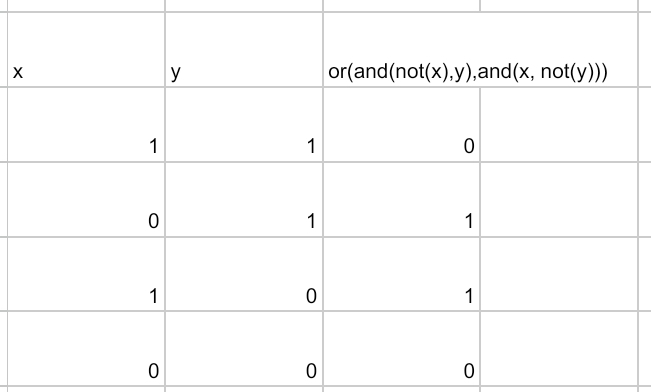
1.Xor: or(and(not(x),y),and(x, not(y)))=xor(x,y)
Truth table:
2.nor: took a while cuz I didn’t think first that nor is just not(or(x,y)). I didn’t connect that to the operators i could use(and, or, not). I think I could do better next time.
3.implies:implies(x,y)=and(or(not(0),0), or(not(0), 0))
truth table:
| x | y | and(or(not(x),y), or(not(x), y)) |
|---|---|---|
| 1 | 1 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 0 | 1 |
I used a website that makes truth tables and this is what I got:
4.equality is and(or(not(x),y), or(x, not(y)))
I just tried the opposite of the expression I made for xor “or(and(not(x),y),and(x, not(y)))”
I generated the expression and this is what I got: