Following Along Async Tutoring [Dface]

[Dface]

@Elliot

try making 3 input nand, nor and xor using operators that take 2 or fewer inputs. for each one, you can stop and give up after 15-30min if it’s hard.

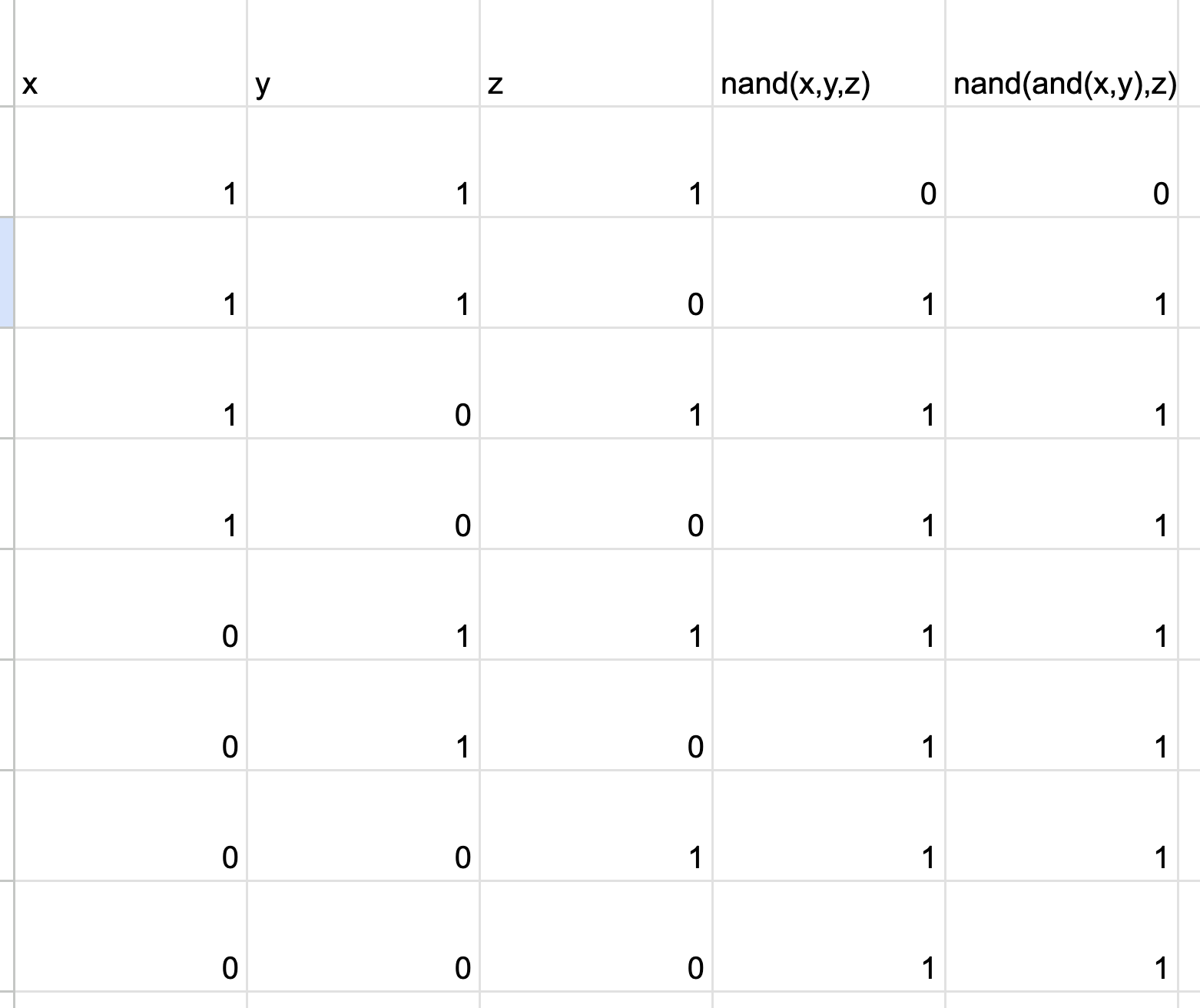
nand(x,y,z) = nand(and(x,y),z):

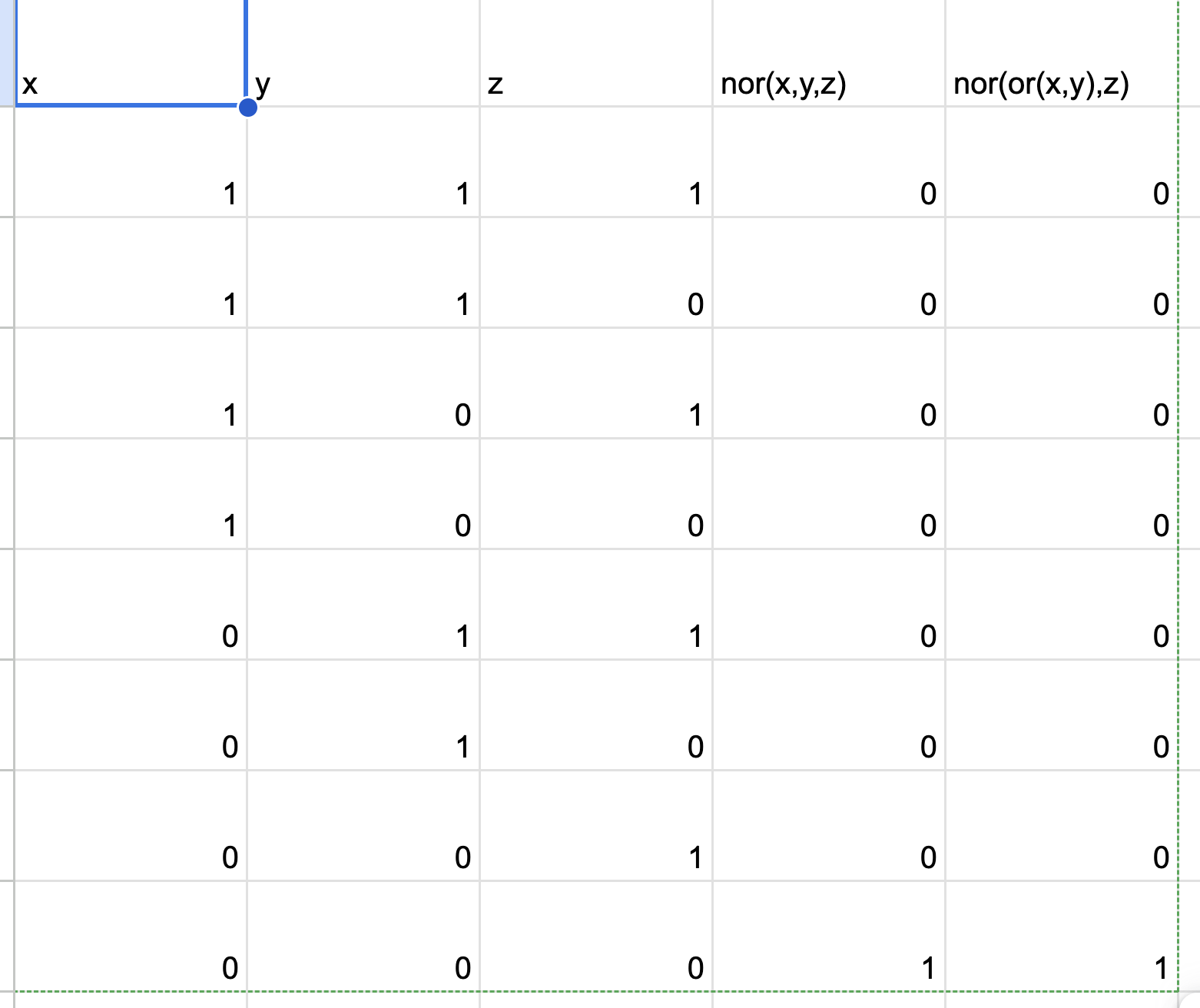
nor(x,y,z) = nor(or(x,y),z):

Couldn’t figure out xor(x,y,z) so I read ahead. I didn’t know actually that an odd number of inputs are true. So three true inputs means the output is true for xor.

I read ahead for more clues and saw this question:

@Elliot

Can you think of a way to check if exactly two inputs are true?

yeah with and(x,y)

I read ahead further and found this:

@Elliot

The context is there are 3 inputs.

You can go through each number (0, 1, 2, 3) and try to think of a way to figure out if exactly that many inputs, out of 3, are true. Give up if you’re stuck too long for each number though.

I was thinking phrasing xor(x,y,z) in english: At least one or three inputs are true.

checking if 0 inputs are true: using only two inputs per operator, it’s nor(or(x,y),z). expression returns true if 0 inputs are true.

checking if 3 inputs are true: and(and(x,y),z). Returns true if 3 of the inputs are true.

I see @Eternity got something similar:

@Eternity

0 and 3 were easy.
For 0 you can use an “or” or “nor” gate. If OR outputs false, all the inputs are false. If NOR outputs true all inputs are false. Regardless you can judge that all three inputs were false.
For 3 you can use an “and” or “nand” gate. If and outputs true, that means all the inputs were true. If nand outputs false that means no input was false, they were all true. Regardless you can judge that all three inputs were true.

I like how nand and or are used to say the same thing. It’s like a way to check the answer twice.

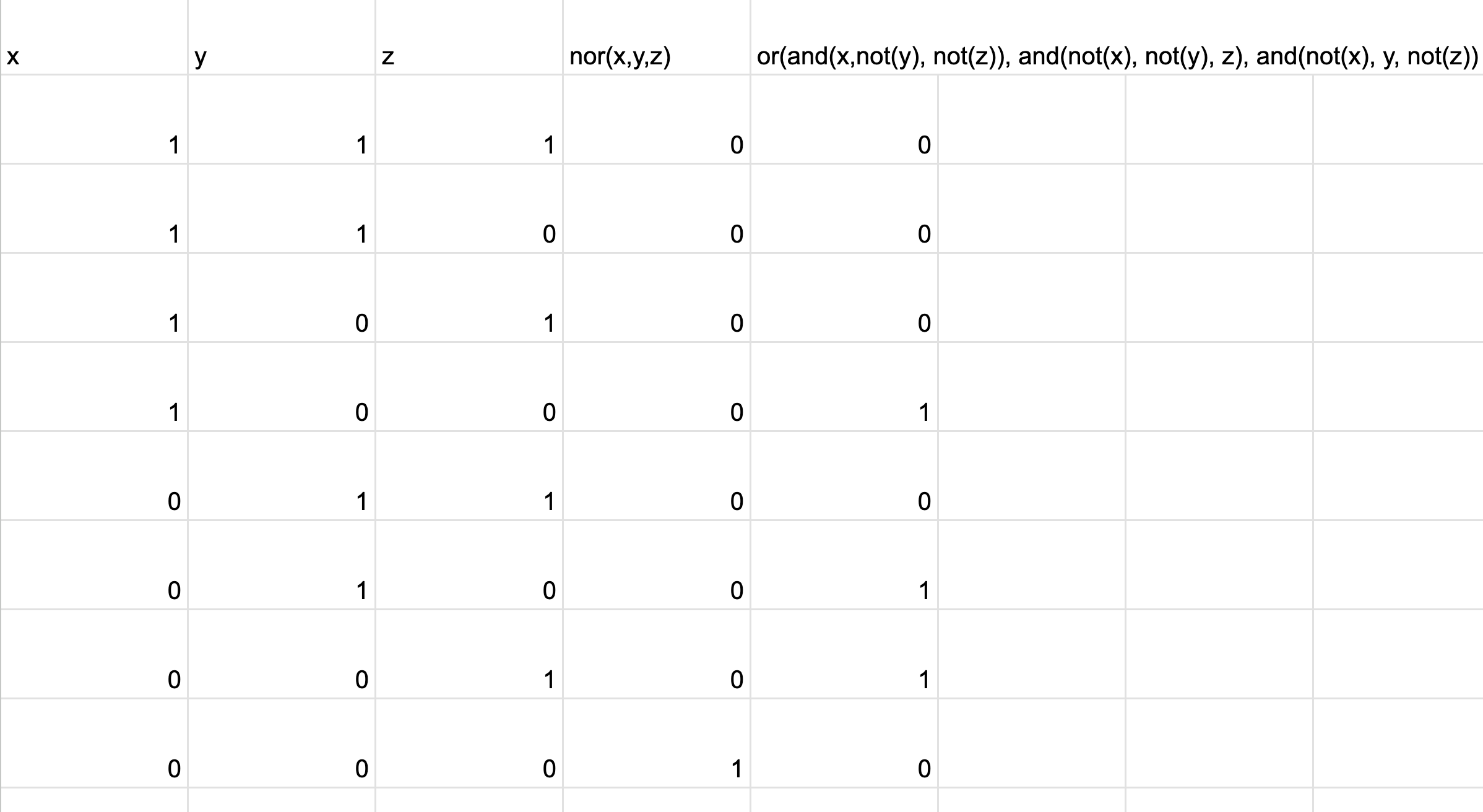
checking if 1 input is true: or(and(x,not(y), not(z)), and(not(x), not(y), z), and(not(x), y, not(z)).
Truth table:

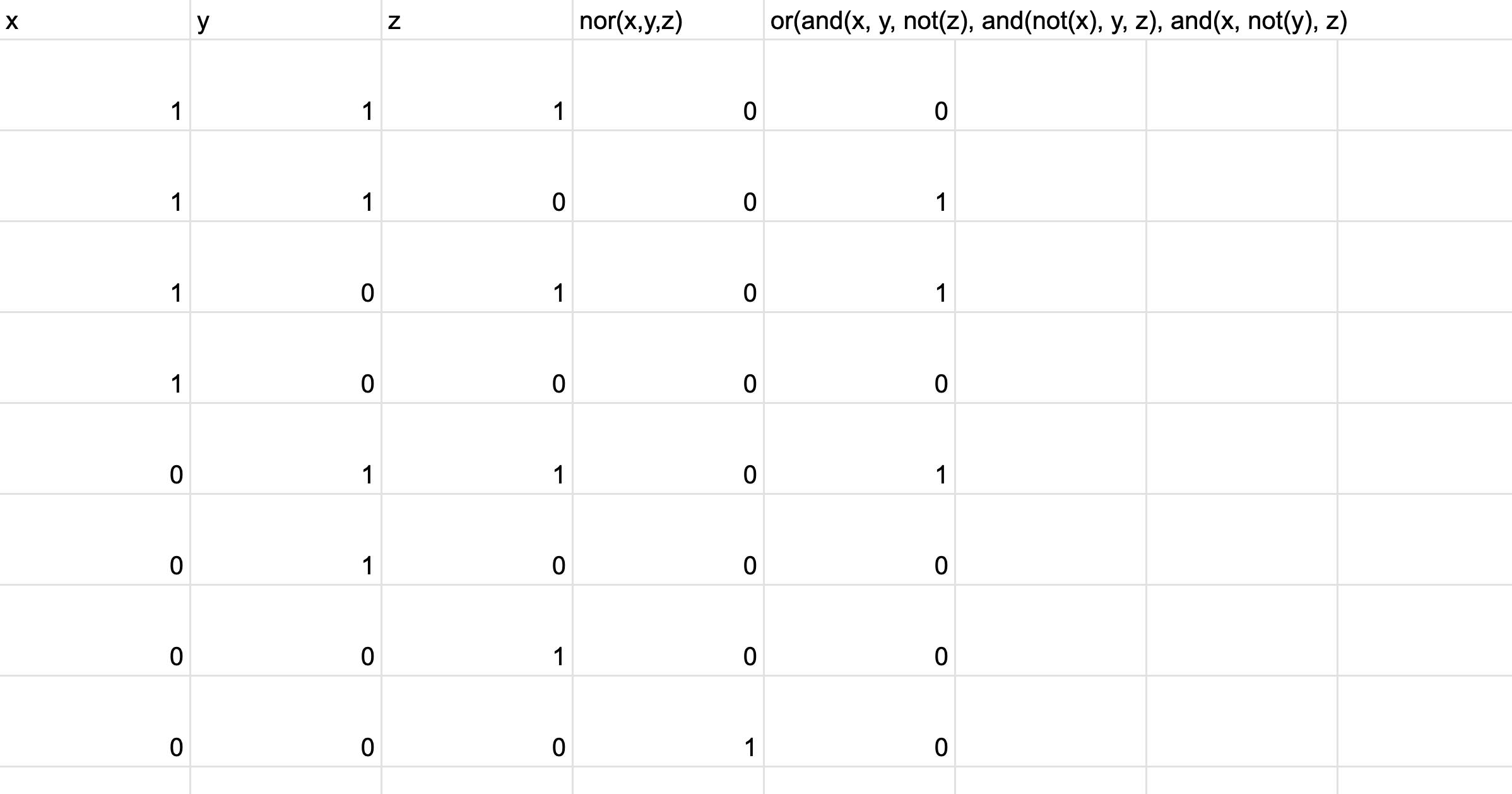
checking if 2 inputs are true: or(and(x, y, not(z), and(not(x), y, z), and(x, not(y, z))
xor(x,y,z)

I think I see what we’re trying to do. If we break down how we find if 1 input is true and 3 inputs are true, then maybe we can find an odd number of inputs being true for xor(x,y,z).