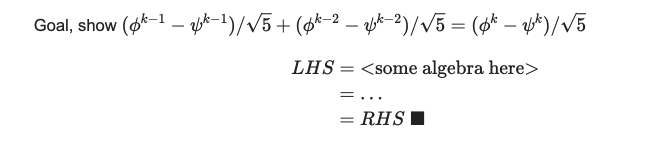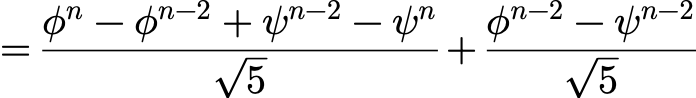Justin Does SICP

Other Friendly
,
41

From https://blog.justinmallone.com/sicp-12-procedures-and-the-processes-they-generate-part-1/

What exactly was the relevance of the golden ratio in understanding the inefficiency of the recursive fibonacci procedure? Quote of relevant material:

In fact, it is not hard to show that the number of times the procedure will compute (fib 1) or (fib 0) (the number of leaves in the above tree, in general) is precisely Fib(n + 1). To get an idea of how bad this is, one can show that the value of Fib(n) grows exponentially with n . More precisely (see exercise 1.13), Fib(n) is the closest integer to \phi^5/\sqrt{n}, where …

From the book (for context):

Exercise 1.13. Prove that Fib(n) is the closest integer to \phi^n/\sqrt{5}, where \phi = (1+\sqrt{5})/2. Hint: let \psi = (1 - \sqrt{5})/2 Use induction and the definition of the Fibonacci numbers (see section 1.2.2) to prove that Fib(n) = (\phi^n - \psi^n)/\sqrt{5}.

I think the point of saying that Fib(n) \approx \phi^n/\sqrt{5} was to show specifically how Fib(n) grows exponentially with n and to ~foreshadow exercise 1.13.

Exercise 1.13 doesn’t seem that useful as a coding exercise, except insofar as rigorously analyzing the complexity of the fib function, via Fib. That skill seems more relevant for like academics and ppl doing theoretical comp sci. That sort of thing doesn’t come up in day-to-day programming (though being able to analyze an algorithms complexity does; in this case the complexity is O(c^n) for some constant c; edit: you don’t need to know what this means; I included it so that you could see the difference between more simplistic day-to-day complexity stuff and like in-depth analysis)

IDK if that answers your q

42

So, my impression was they were bringing up the golden ratio cuz it was supposed to be illuminating re: what they were talking about, and that since I’m only vaguely familiar with the golden ratio, I lacked whatever intuitions they were trying to conjure up in the mind of the reader that were suppose to be illuminating. And so the thought behind my question was kind of “what am I missing?” So you didn’t quite answer it but to be fair it’s kind of a hard question and I appreciate the attempt :slight_smile:

43

BTW part of the reason for putting unanswered questions down is just as an honest acknowledgement of what I don’t know, which I think has some value regardless of whether a particular question gets answered

44

Ahh, I think I see what you mean. re: illuminating, I think it’s just a bit of maths trivia. the fibonacci sequence and the golden ratio are connected in many ways. e.g., if you pick two large adjacent fibonacci terms (like 14930352 and 24157817), then their ratio will approach \phi the further in to the sequence you go – the ratio of those two terms is 1.61803… for example. So mb the author thought it was fun to share some extra connections between the fibonacci sequence and \phi.

Actually, thinking more about it now, the book is saying that the number of leaves in the tree of (fib n) is Fib(n+1) (which is interesting b/c fib is an implementation of Fib). so the number of leaves in the tree of (fib n) is also the result of (fib (+ n 1)). That seems like a ‘fun fact’ kind of thing that authors would put in there. Since Fib(n) \approx \phi^n/\sqrt{5}, this means that there’s \sim \phi^{n+1}/\sqrt{5} leaves in the tree of (fib n), which grows exponentially.

45

Ah that’s pretty cool about the ratio of big Fibonacci numbers approaching \phi

46

I was looking for other people’s answers for Exercise 1.10. E.g. @AnneB has one here:
https://aelanteno.github.io/sicp-exercises/exercise-1.10
And this guy has one:

They used a different notation than I did - like more standard exponent notation but with what I think is some composition of functions. I find it harder to follow. I think AnneB tries to show some of the steps but I didn’t follow them very well.

I think i liked the Rudy Rucker notation I found cuz it matched my intuitions well (about having a “tower of exponentiation” that includes the “bottom” value in the tower of stuff being repeatedly exponentiated). It seems worth maybe trying to think about stuff in different ways though.

47

having some kinda issue with Exercise 1.11.

image
image1452×344 34.8 KB

so recursive was pretty easy for me (i named it fr cuz the r stands for recursive here)

(define (fr n)
  (if (< n 3) n
      (+
       (fr (- n 1))
       (* 2 (fr (- n 2)))
       (* 3 (fr (- n 3))))))

i’m having some trouble translating this into iterative version though.

i made a tree of some example operations with this function’s recursive implementation to understand how it works more ( (f 7) is abbreviated)

Exercise 1-11
Exercise 1-118054×3080 738 KB

I’ve gotten stuck trying to translate from a recursive process to an iterative process. for now, my plan is to finish watching a couple of videos on this material (MIT guys have one, as does Brian Harvey) and then take another stab at it. Also I’m planning on looking carefully at the factorial example in the book (where they implement a function for finding factorials both recursively and iteratively) to see if I can describe a general method of going from a recursive to iterative process or some general principles or whatever. Thoughts welcome. I think it’s kind of interesting that I found the recursive form really intuitive and am finding the iterative form kinda difficult.

48

I looked at it as writing an iterative process from scratch, not translating a recursive process to an iterative one. Maybe that would help you.

I too find it easier to write Scheme programs recursively than iteratively. I don’t know if that’s because I’ve had more experience doing it that way or because Scheme is somehow set up to make recursion more natural.

49

figured it out :raised_hands::tada:. What I wrote on this to figure things out is pasted below

Let’s start with (fi 3) (the “i” standing for iterative).

For (fi n) where n = 3:

(fi (- n 1)) = (fi 2) = 2
(fi (- n 2)) = (fi 1) = 1
(fi (- n 3)) = (fi 0) = 0

To figure out (fi 3), we want sum up (fi 2) (or 2), 2 multiplied by (fi 1) (or 2), and 3 times (fi 0) (or 0). We get a total of 4 from doing this.

Suppose we want to figure out (fi 4). To figure out (fi 4), we’ll need the values of (fi 3), (fi 2), and (fi 1). When n = 3 for (fi n), those values are:
for (fi 3), the sum of (fi 2), 2 times (fi 1), and 3 times (fi 0). This is 4.
for (fi 2), the value of (fi (- n 1), which is 2.
for (fi 1), the value of (fi (- n 2), which is 1.

So within (fi 3), we can generate all the values we need for calculating (fi 4).

We could think of there being three key values. For a given n, there is the value of fi one step back (fi (- n 1), and the value of fi two step backs, and the value of fi three steps back ((fi (- n 2)).

We might call these 1ago, 2ago, and 3ago.
For (fi 3), these values are 2, 1, 0.
For (fi 4), these values are 4, 2, 1.
For (fi 5), these values are 11, 4, 2.
For (fi 6), these values are 25, 11, 4.
For (fi 7), these values are 50, 25, 11.

Notice that a new value is generated using the existing values in the first slot (for 1ago), and then that value recurs as we increase n by 1, first as 2ago, then as 3ago.

In order to have an iterative procedure that can solve Exercise 1.11 for arbitrary values, we will want to do a recursive call to that iterative procedure with appropriate transformations of these values.

So, suppose we start at a calculation of (fi 3) as our initial starting place with initial values of 2, 1, 0 for 1ago, 2ago, 3ago. How will we transform these values into a suitable form for calculating (fi 4)?

As our new 1ago argument, we’ll want to provide (+ 1ago (* 2 2ago)(3 3ago)). This is 4.
As our new 2ago argument, we’ll want to provide our current 1ago argument, which is (fi 2) or 2.
As our new 3ago argument, we’ll want to provide our current 2ago argument, which is (fi 1) or 1.

With these values provided, our procedure will be able to calculate (fi 4) by engaging in the appropriate transformations of them per the rule specified in the exercise.

I went awry partially cuz I was doing unnecessary operations because I hadn’t thought in sufficient detail about which operations were necessary. He’s some mistaken code that that I wrote:

;bad wrong code; not the answer!

(define (fi n)
  (if (< n 3) n
      (fi-helper 2 1 0 3 n)))

(define (fi-helper 1ago 2ago 3ago current max)
  (if (= current max)
      (+ 1ago (* 2 2ago) (* 3 3ago))
      (fi-helper
       (+ 1ago 2ago 3ago) ;WRONG!
       (* 2 1ago)   	  ;WRONG!
       (* 3 2ago)         ;WRONG!
       (+ current 1)
       max)))

Multiple problems here.
One is that, for some reason, I’m doing a different operation on the numbers in my recursive call to fi-helper (specifically, (+ 1ago 2ago 3ago)) than I do as the consequent for the if (specifically, (+ 1ago (* 2 2ago) (* 3 3ago)). It was only after going through and writing all the stuff above that I realized clearly that these should be the same operation, and specifically that they should be (+ 1ago (* 2 2ago) (* 3 3ago)).
The second issue is that I am unnecessarily multiplying the 1ago and 2ago values by 2 and 3, respectively, in providing them as arguments for my recursive call. Going through the above analysis helped me realize that these values should be left untouched.

Below is a fixed and functioning fi program. Note that I also keep track of which n value we’re currently calculating (using current) and the final n we need to reach (with max).

(define (fi n)
  (if (< n 3) n
      (fi-helper 2 1 0 3 n)))

(define (fi-helper 1ago 2ago 3ago current max)
  (if (= current max)
      (+ 1ago (* 2 2ago) (* 3 3ago))
      (fi-helper
       (+ 1ago (* 2 2ago) (* 3 3ago))
       1ago
       2ago
       (+ current 1)
       max)))

EDIT: trying to write things out really explicitly and precisely was helpful. i was mixing up what I was supposed to do when and was getting myself confused.

Mindmap helped too but sometimes I just really need to write 500-1k words and see if stuff clicks after doing that.

50

is it even a coding exercise at all? it seems like they’re asking for more of a math proof

51

Also, what do u actually need to know math-wise to solve 1.13

52

No. It’s like maybe late high-school advanced (like calculus) maths level.

quality-of-life link back up to 1.13

Not that much really. The problem tells you to use induction so you start with evaluating the base case (n=1) for Fib(n) = (\phi^n - \psi^n)/\sqrt{5}. Since we need to use the definition Fib(n) = Fib(n-1) + Fib(n-2) we probably need a 2nd base case too, for n=2. Then the goal is to show that the formula works for some n=k assuming that it already works for n=k-1 and n=k-2. I’d lay that out like:

Goal, show (\phi^{k-1} - \psi^{k-1})/\sqrt{5} + (\phi^{k-2} - \psi^{k-2})/\sqrt{5} = (\phi^k - \psi^k)/\sqrt{5}

\begin{aligned} LHS & = \text{<some algebra here>} \\ & = \dots \\ & = RHS \; \blacksquare \end{aligned}

once you show that the base cases work, and that the case n=k works provided that n=k-1 and n=k-2 work, then you’re done with the proof by induction (because if it works for n \in \{1,2\} then it must work for n=3, so it must also work for n=4, … etc).

The last bit of the exercise (which is actually the first sentence) is to show that Fib(n) is the closest integer to \phi^n/\sqrt{5}. Since we know Fib(n) = (\phi^n - \psi^n)/\sqrt{5}, one way to do that is show that -0.5 \le \psi^n/\sqrt{5} \le 0.5 which is fairly straight forward once you write it out. Note that \lim_{n \to \infty} \psi^n = 0 as |\psi| < 1.

53

I think maybe this is what you meant by evaluating base cases but I’m not sure. Feel free to correct me

Fib(1) = 1 per our definition of Fib(n)
So we want to show that
\frac{\phi^1 - \psi^1}{\sqrt{5}} = 1
Step 1: \frac{\phi^1 - \psi^1}{\sqrt{5}}
Step 2: \frac{1}{\sqrt{5}}(\frac{1 + \sqrt{5}}{2} - \frac{1 - \sqrt{5}}{2})
Step 3: \frac{1}{\sqrt{5}}{(\frac{2\sqrt{5}}{2})}
Step 4: 1

So Fib(2) = 1 per our definition of Fib(n).
So we want to show that:
\frac{\phi^2 - \psi^2}{\sqrt{5}} = 1

Step 1: \frac{\phi^2 - \psi^2}{\sqrt{5}}
Step 2: \frac{(\phi - \psi)({\phi + \psi})}{\sqrt{5}}
Step 3: \frac{1}{\sqrt{5}}{(\phi - \psi)({\phi + \psi})}
Step 4: \frac{1}{\sqrt{5}}{( \frac{1 + \sqrt{5}}{2} - \frac{1 - \sqrt{5}}{2})({\frac{1 + \sqrt{5}}{2} + \frac{1 - \sqrt{5}}{2}})}
Step 5: \frac{1}{\sqrt{5}}{(\frac{2\sqrt{5}}{2})({\frac{2}{2}})}
Step 6: 1

54

Yup, exactly. Nice finding the difference of two squares, too (I just expanded it, which is messier). :+1:

55

btw i noticed that Discourse seems to strip the mathjax-indicator $ signs when you quote math stuff for a reply; wonder if there’s an easy way to fix that on an automated basis

56

hmm not really sure how to do this step. spent some time trying playing around with algebra but idk what to do yet

btw I did part of this quote as an image cuz i didn’t want to fix the mathjax syntax

57
If you want a hint

evaluate:

  1. \phi^2
  2. \phi + 1
  3. \psi^2
  4. \psi+1

I googled for a hint (it’s tricky without knowing the above). after you know those bits it was much more straight forward to show LHS = RHS.

Yeah, good idea.

58

Well I tried for a while but couldn’t figure it out.

I’m looking at answers. I’m trying to understand AnneB’s at the moment, at the point where she says:

replace one ɸ * ψ with -1 in each of the two middle terms of the top half of the first fraction, since ɸ * ψ = -1:

image
image696×98 4.1 KB

I notice that for the middle values in the left fraction’s numerator, the difference in the exponent increased by 1 (going from (n-1) to (n-2)) compared to the previous step. I’m not crystal clear on why that’s happening.

59

My soln:

Goal: given the inductive hypothesis, show that

\begin{align} \frac{\phi^{k-2}-\psi^{k-2}}{\sqrt{5}} + \frac{\phi^{k-1}-\psi^{k-1}}{\sqrt{5}} & = \frac{\phi^{k}-\psi^{k}}{\sqrt{5}} \\ \text{} \\ \text{i.e.,}\;\;\phi^{k-2}-\psi^{k-2} + \phi^{k-1}-\psi^{k-1} & = \phi^{k}-\psi^{k} \end{align}

Note:

\begin{align} \phi^2 & = (\frac{1 + \sqrt{5}}{2})^2 \\ & = \frac{6 + 2\sqrt{5}}{2^2} \\ & = \frac{3 + \sqrt{5}}{2} \\ & = 1 + \frac{1 + \sqrt{5}}{2} \\ & = 1 + \phi \end{align}

Similarly:

\psi^2 = 1 + \psi

The proof

\begin{align} LHS & = \phi^{k-2}-\psi^{k-2} + \phi^{k-1}-\psi^{k-1} \\ & = \phi^{k-2}(1 + \phi) - \psi^{k-2}(1 + \psi) \\ & = \phi^{k-2}\cdot\phi^2 - \psi^{k-2}\cdot\psi^2 \\ & = \phi^{k} - \psi^{k} \\ & = RHS \;\;\; \blacksquare \end{align}
60

Yeah, so before that step, the numerator of the first fraction is

\begin{align} & = \phi^n + \phi^{n-1}\psi - \phi\psi^{n-1} - \psi^n \\ & = \phi^n + \phi^{n-2}(\phi\psi) - (\phi\psi)\psi^{n-2} - \psi^n \\ & = \phi^n - \phi^{n-2} + \psi^{n-2} - \psi^n \\ & = (\phi^n - \psi^n) - (\phi^{n-2} - \psi^{n-2}) \\ \end{align}

The second bracketed part then cancels with the numerator of the second fraction.

BTW, I really like Anne’s soln. The extra fact I used makes sense to find because you do some of the operations calculating Fib(2), but I think Anne’s is more creative.