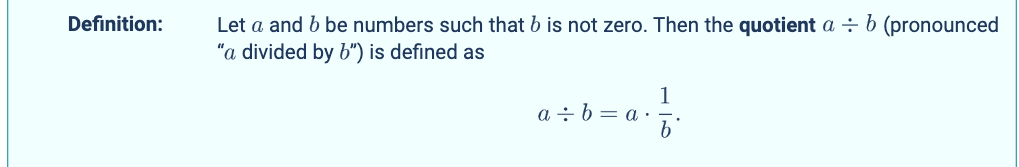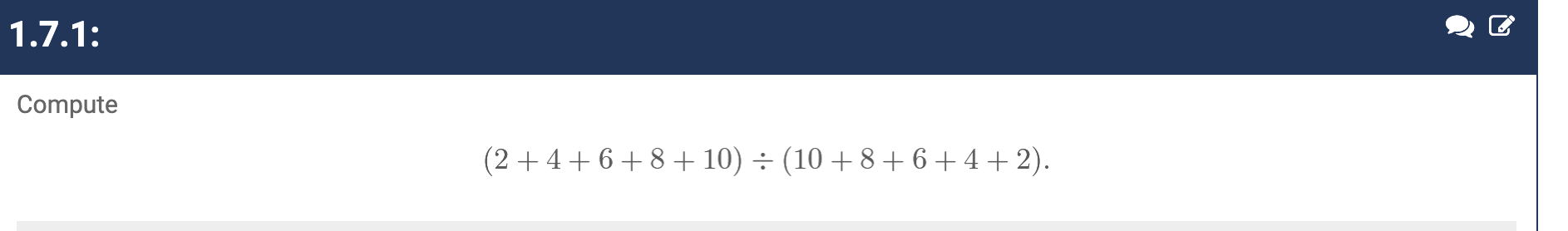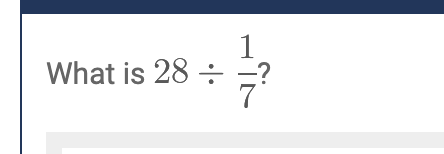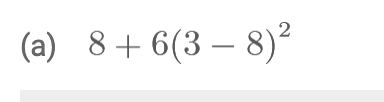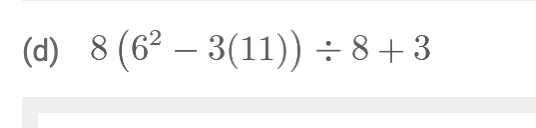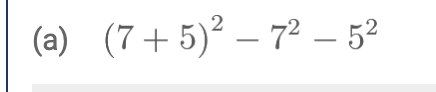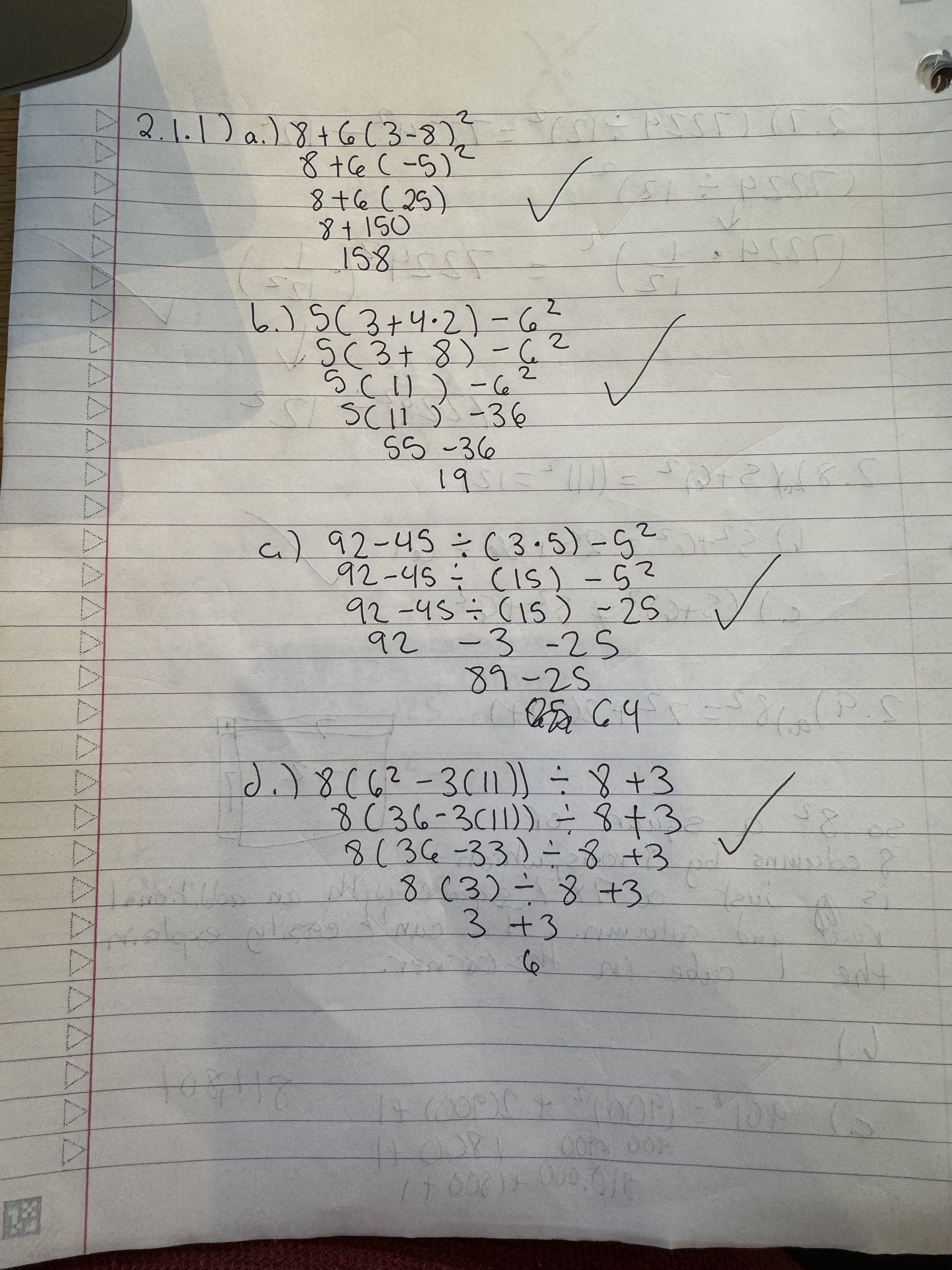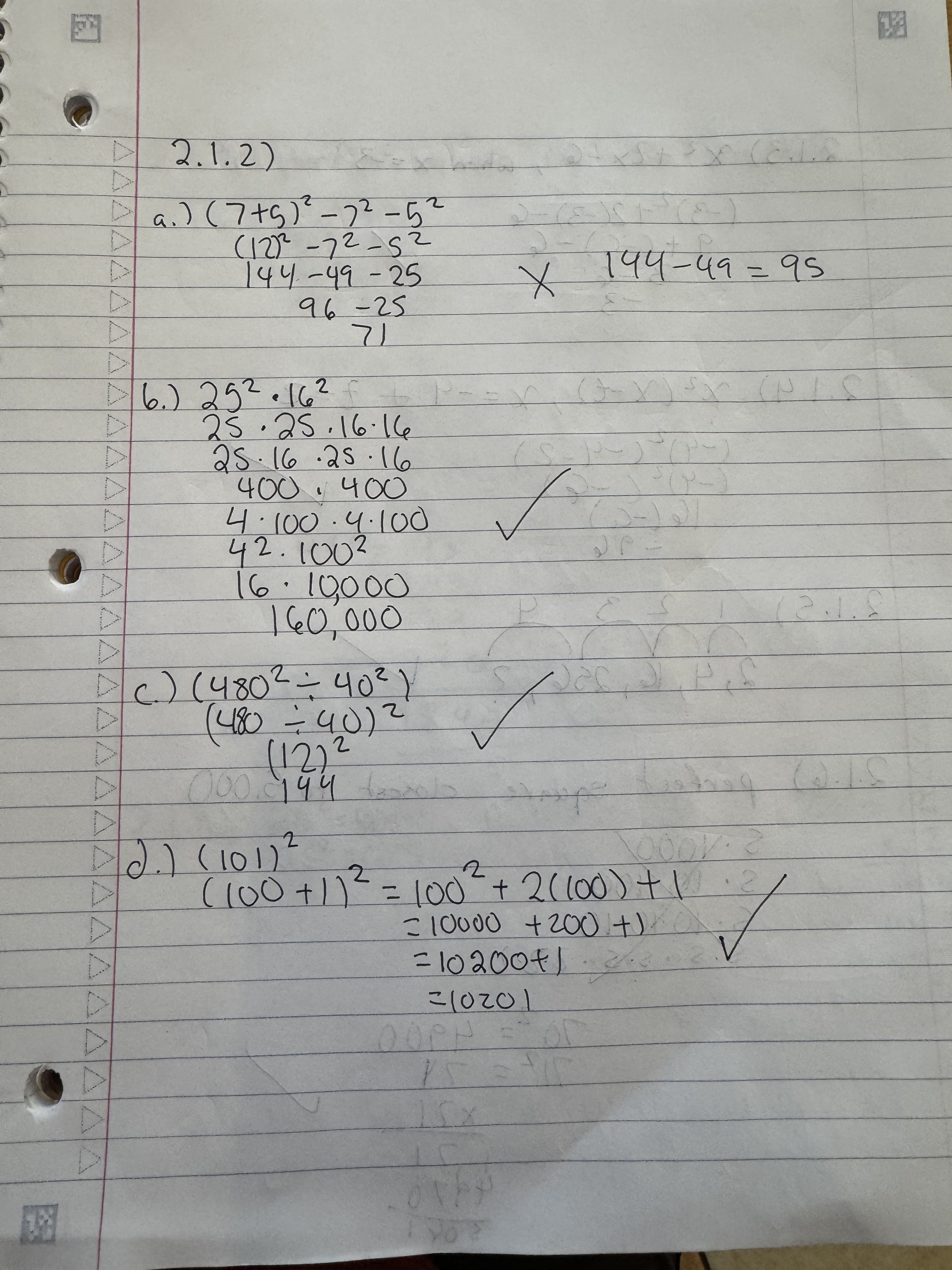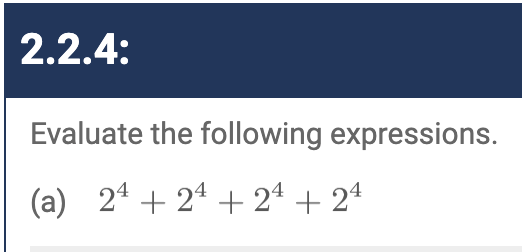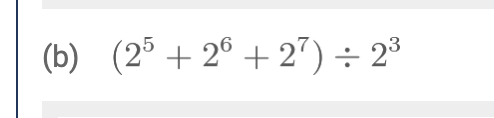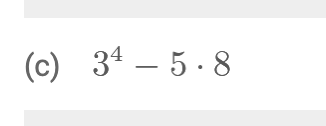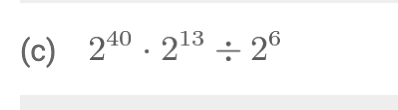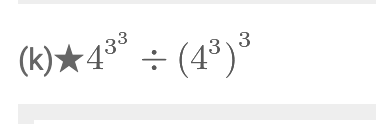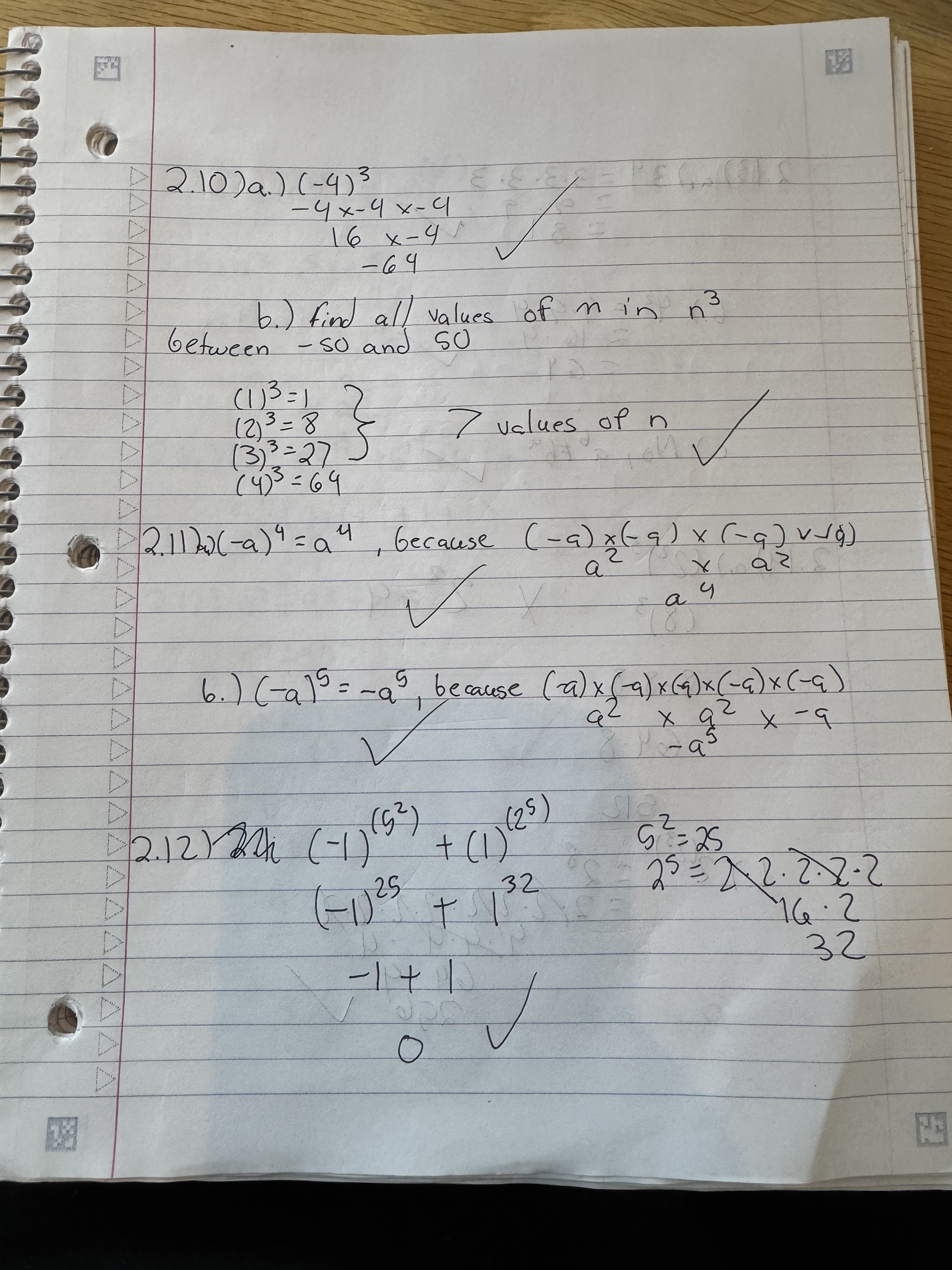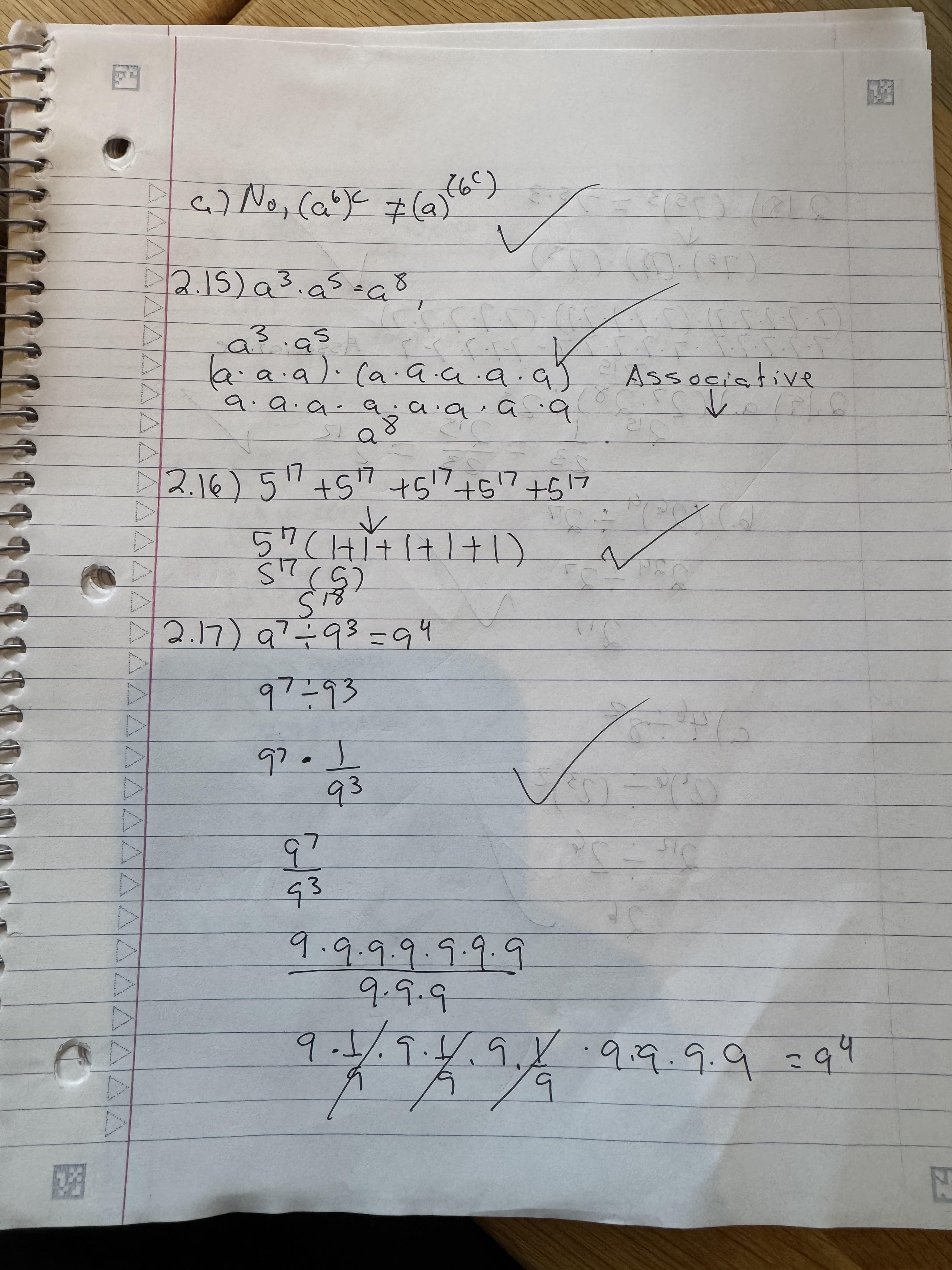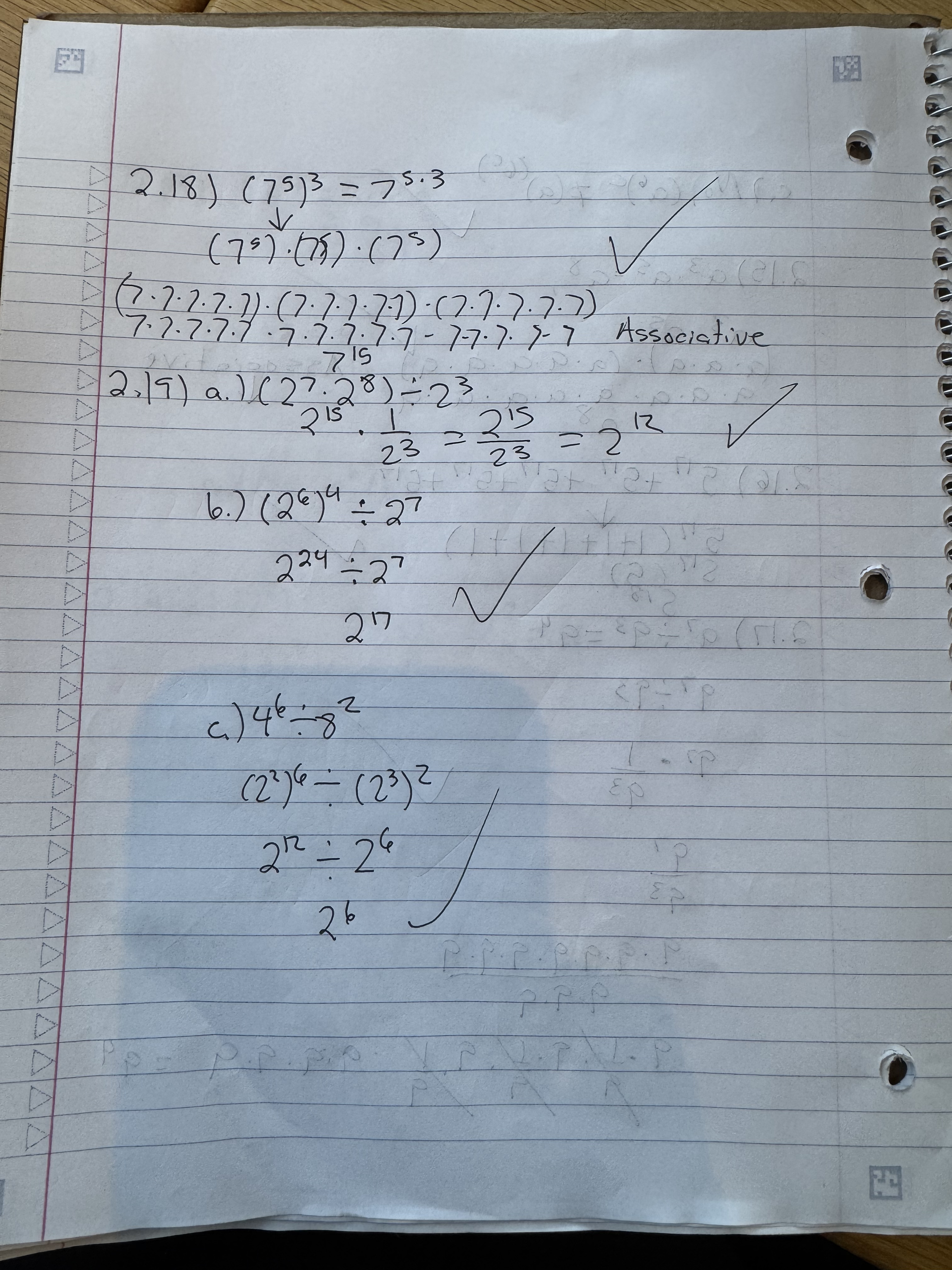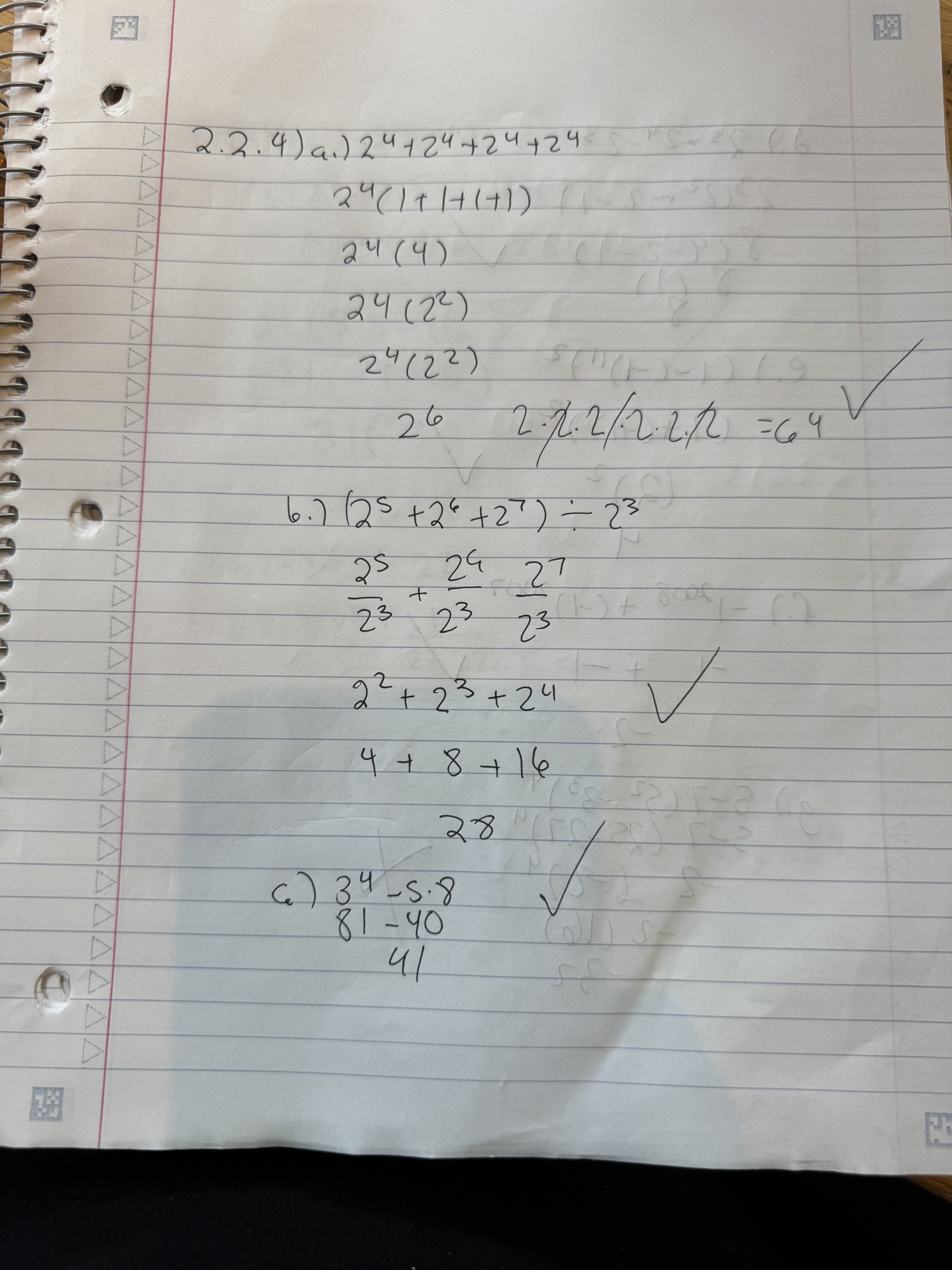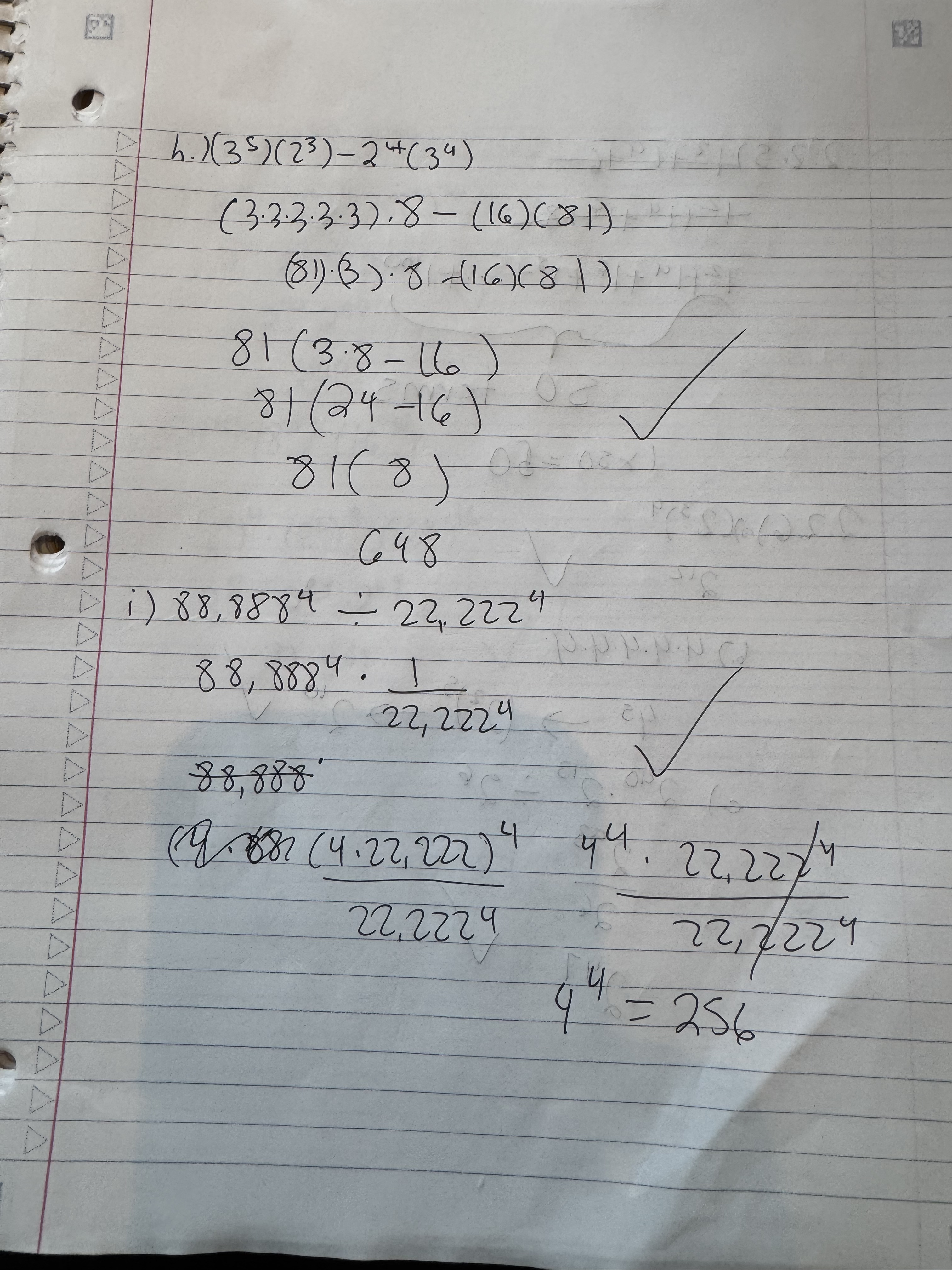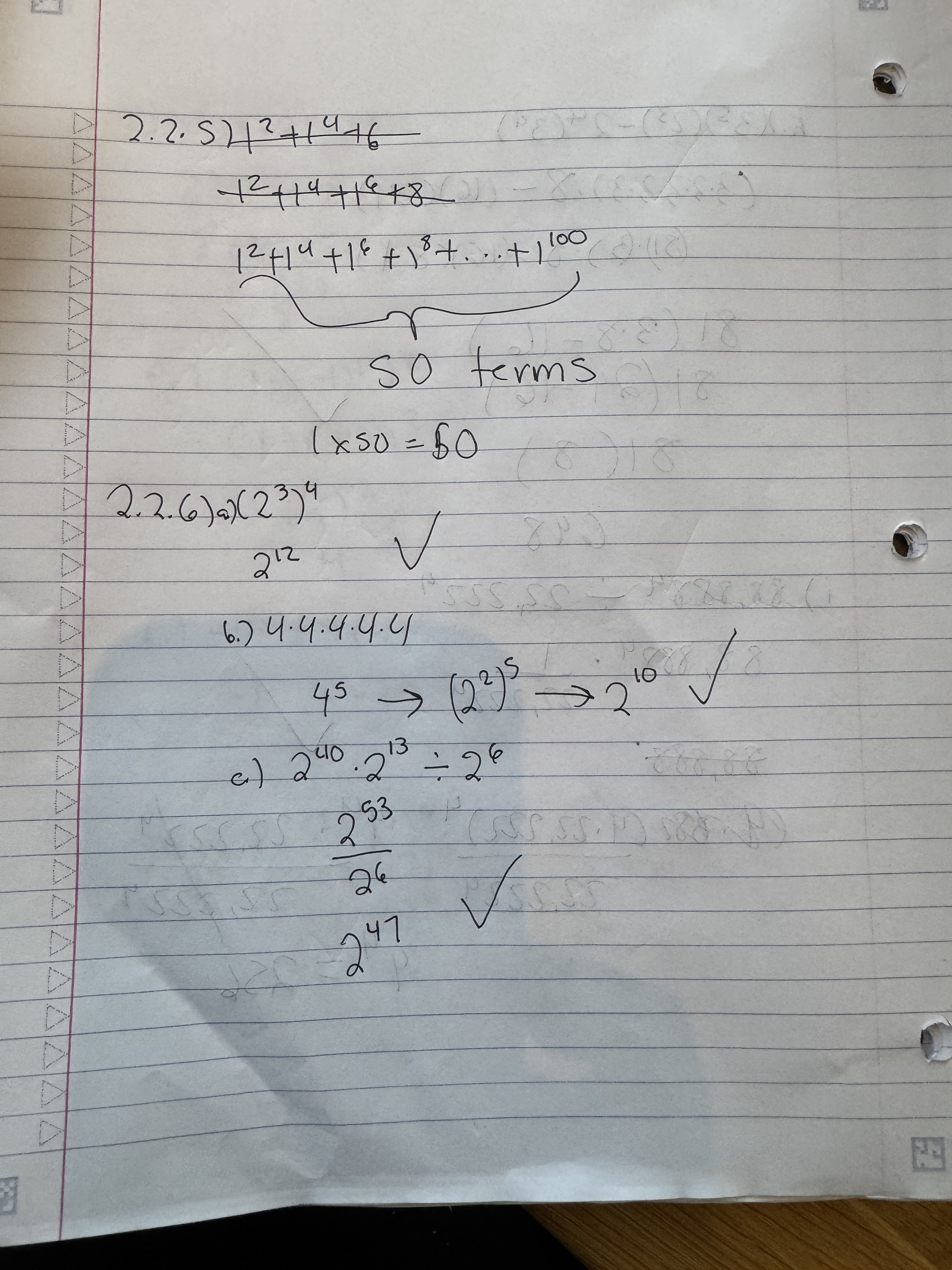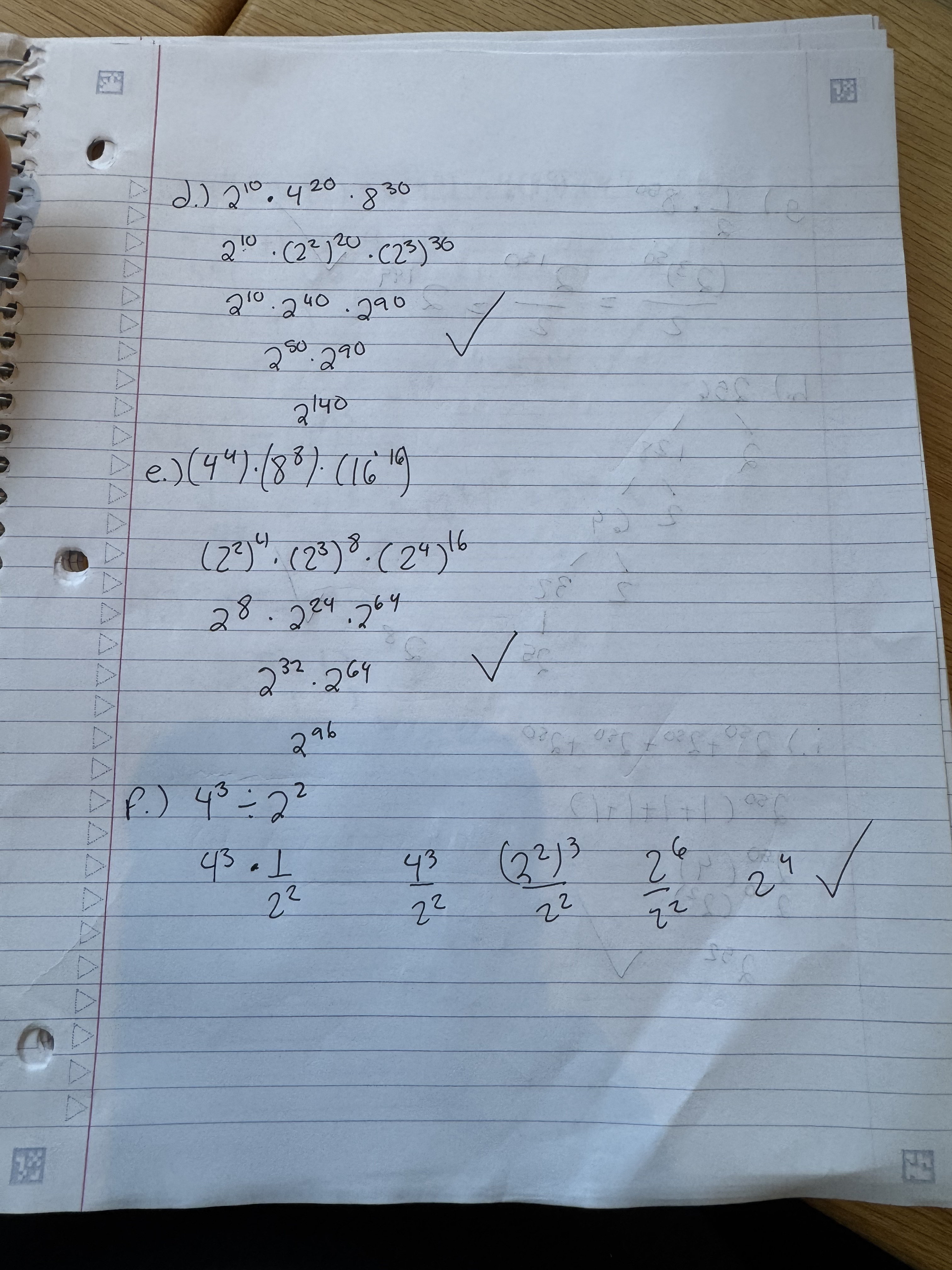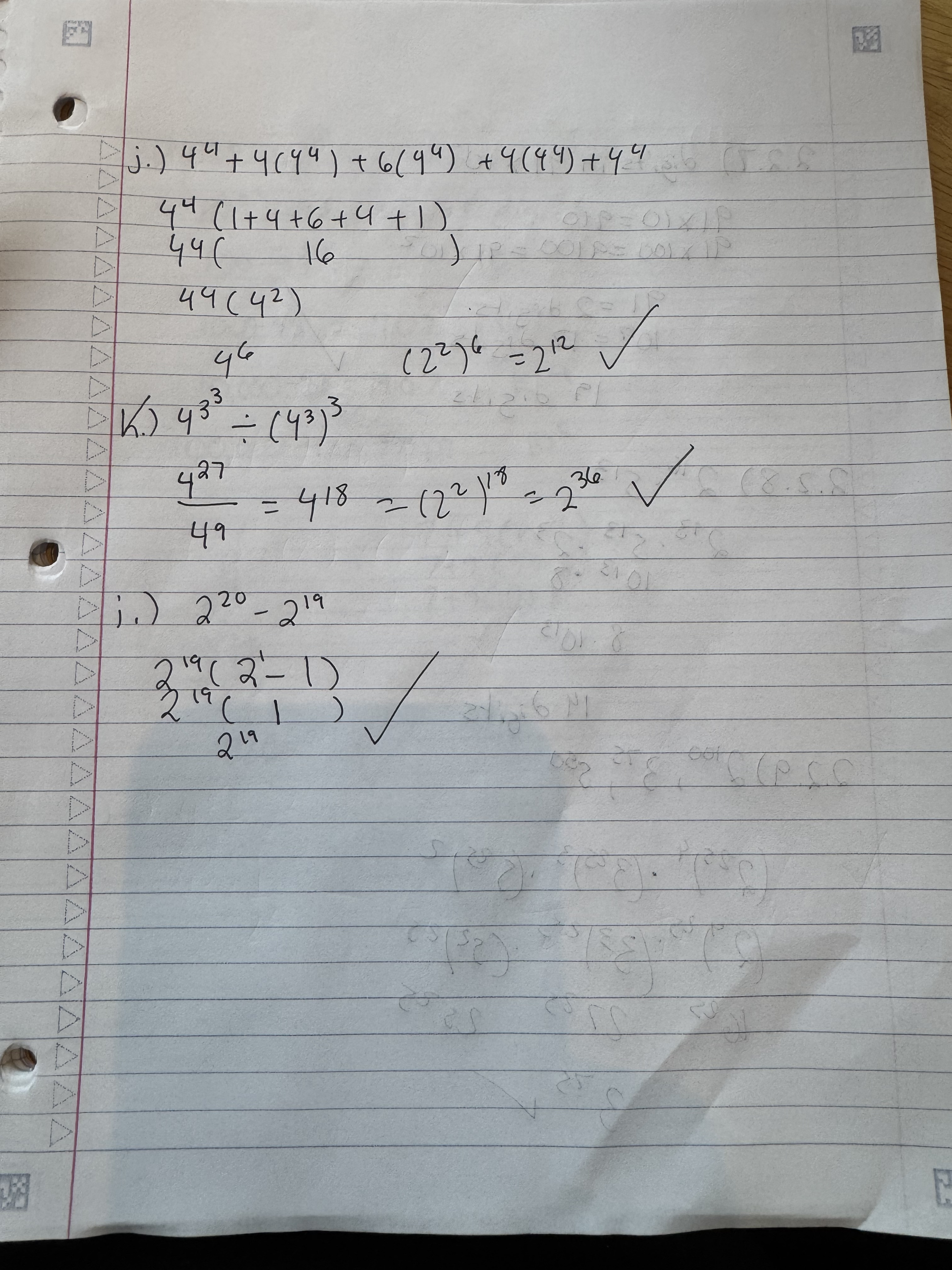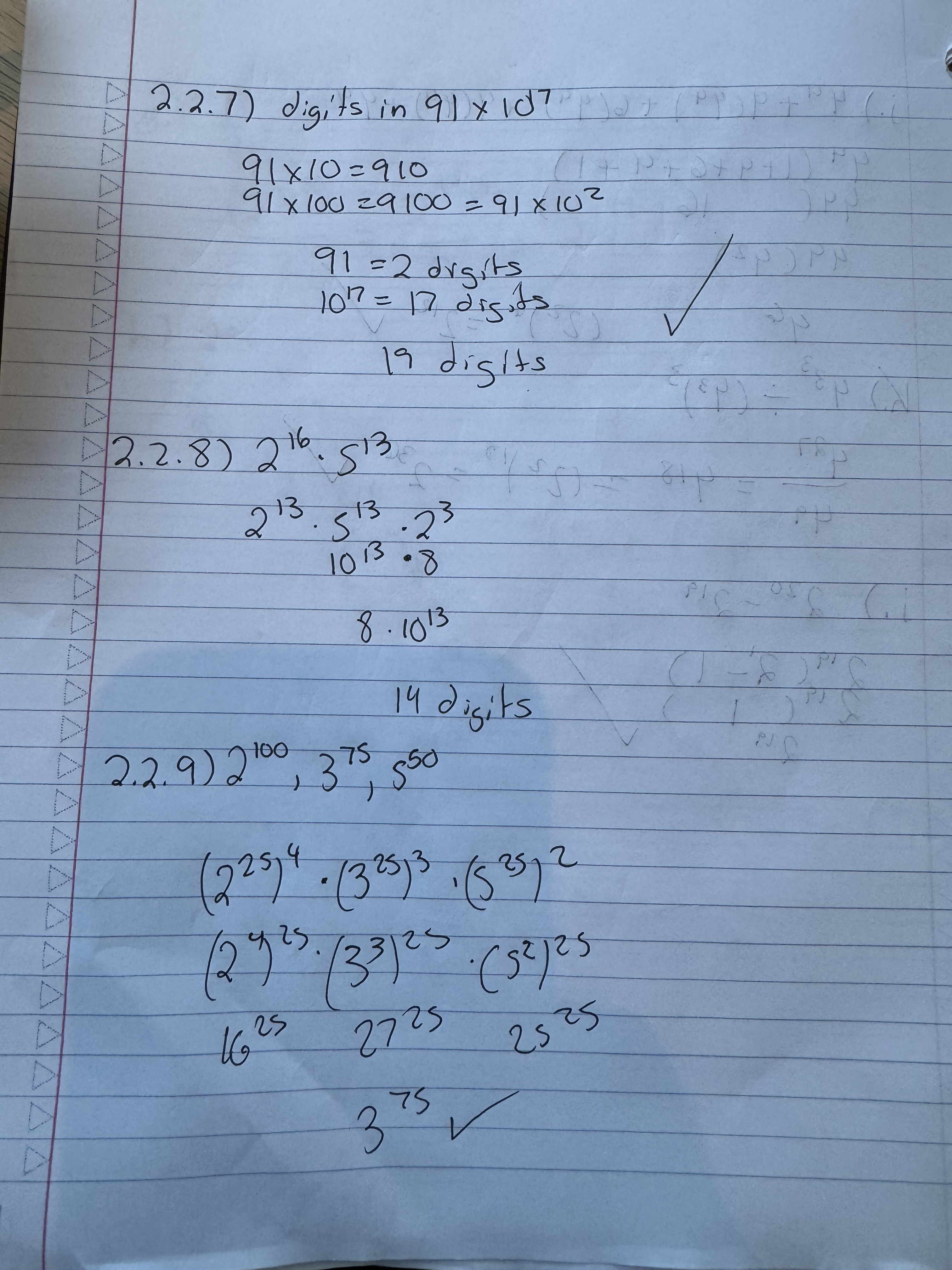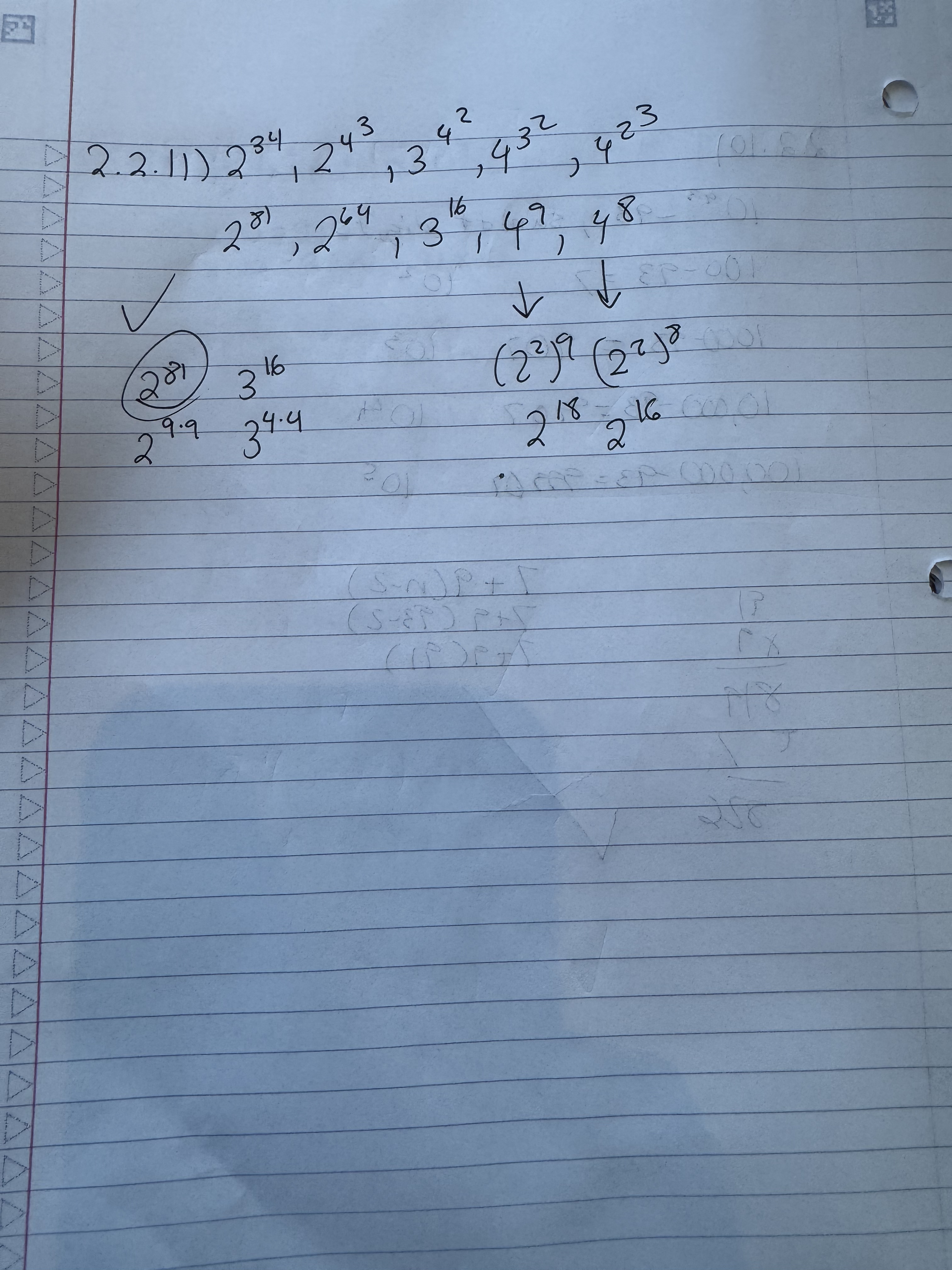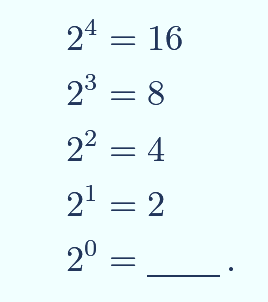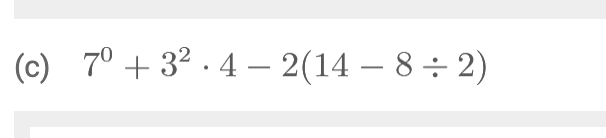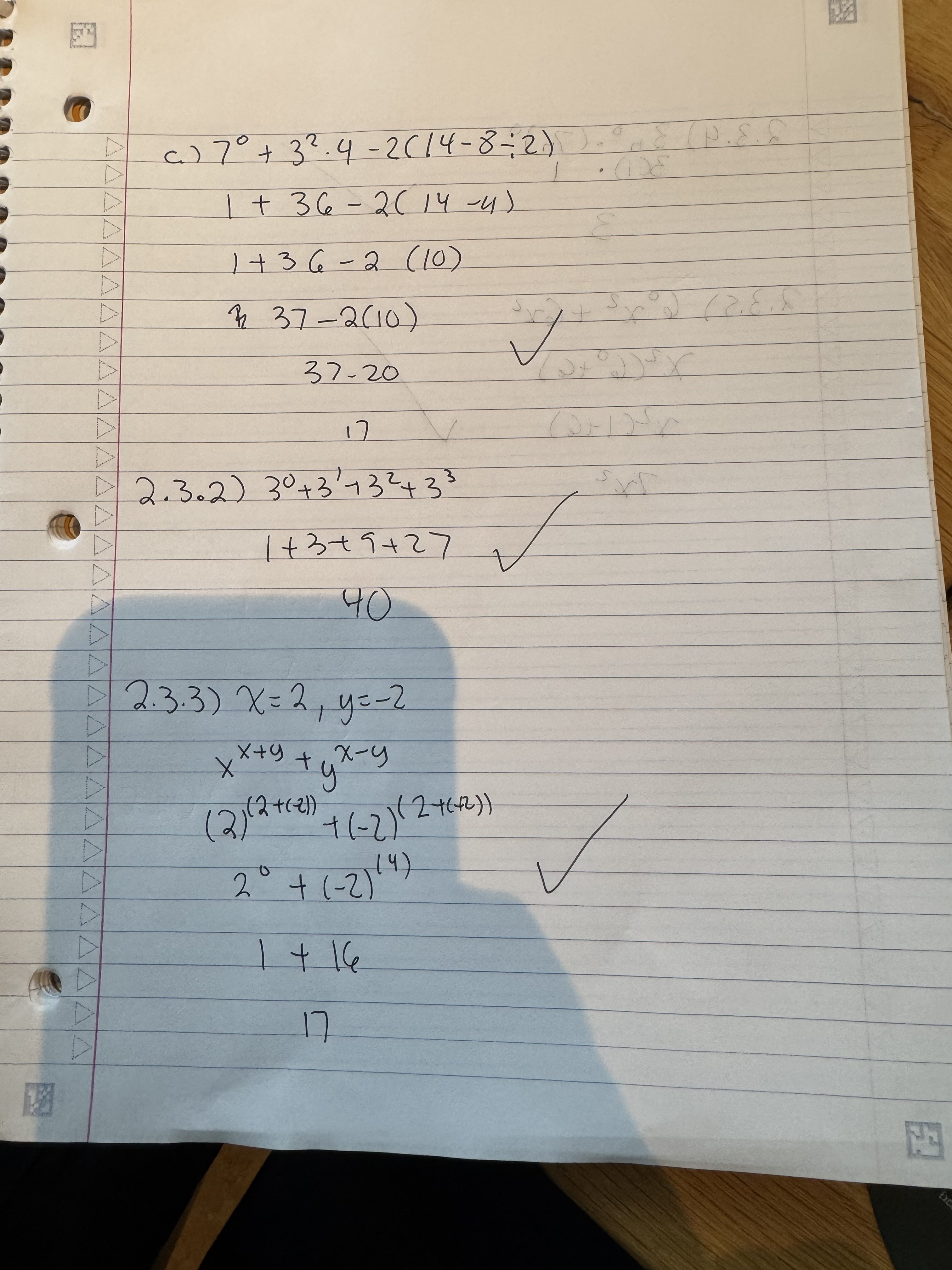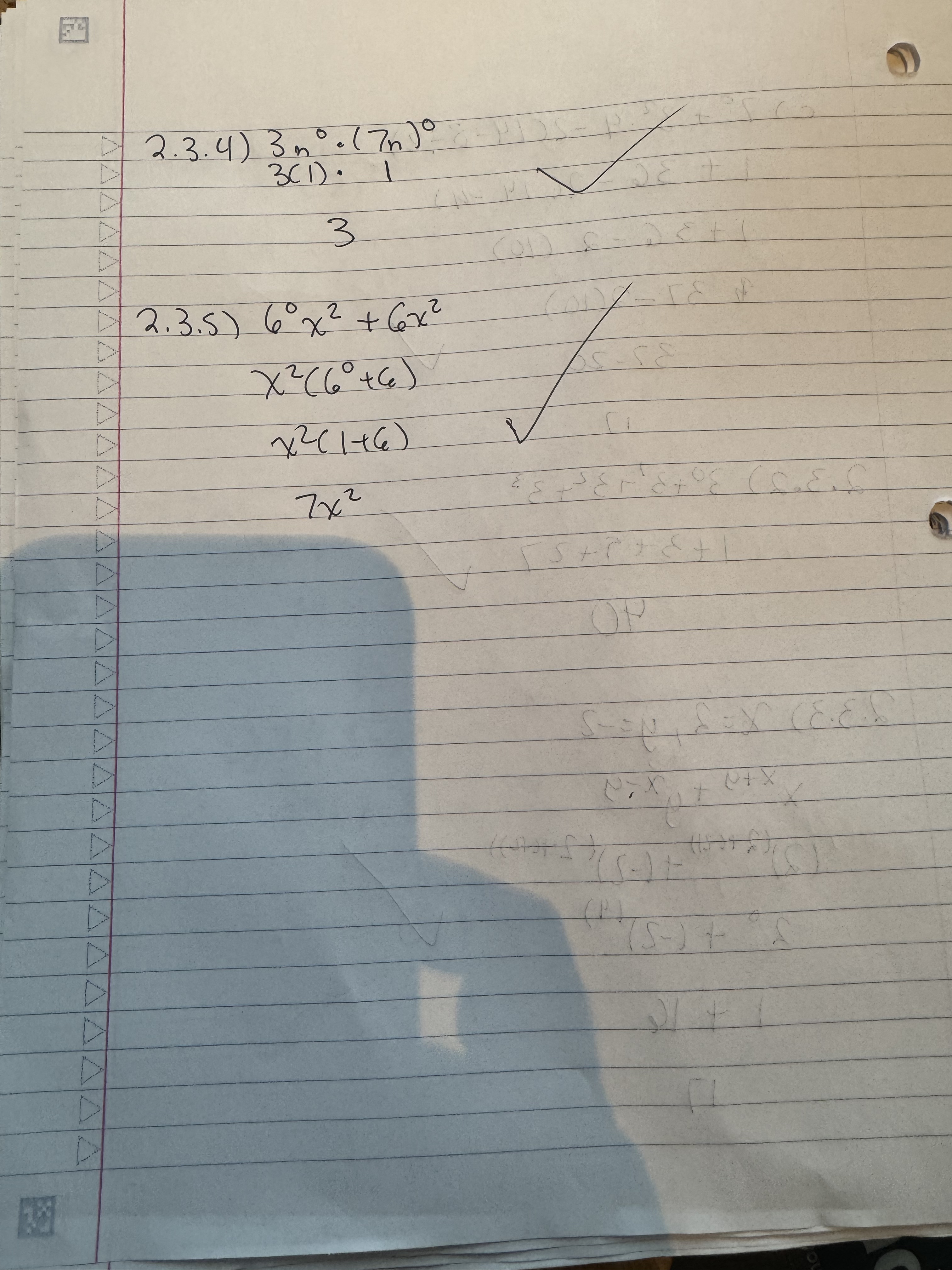Do you mean bothered like you think they did something bad (I don’t see it) or bothered like you wanted to think about it more, analyze it more, understand it more?
Kinda more the second point about thinking about it more and stuff. This wasn’t too deep a point.
So they start off talking about the addition identity, then we talk about the multiplication identity, then it goes to (italics added) “But the question we really want to ask is”. Why is that the question we really want to ask? Sure multiplication has an identity. What does that have to do with wanting to figure out whether there’s a number times x that equals 1?
1.7 Division
We’d like a more general definition of division, but one that gives the same answers as our simpler way of thinking about division. Recall how we defined subtraction in Section 1.5 as a combination of addition and negation.
In other words, dividing by a number means multiplying by its reciprocal.
In other words instead of dividing A by B, we multiply A times the reciprocal of B. It now becomes A x 1/B.
Skipped the beginning chapter problems. Got all the exercises right.
1.8 Summary
2.1 Squares
So in 56 , 5 is the base and 6 is the exponent. We multiply the base an exponent number of times against it self.
So not all squares are perfect squares? Oh a perfect square refers to the answer you get from a square. And a perfect square refers to the squares of integers. Ok. Idk. whats wrong with the square from squaring 2.1?
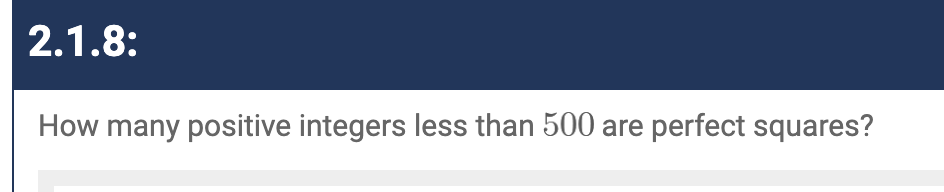
I did a few beginning of chapter problems this time:
I did this to get some practice with (-2)2 vs -22 . I confuse the two a lot. I got this correct.
Solution
Ok that’s pretty neat. I didn’t notice that. That also makes sense from looking at (a+1)2 . Its a number, a, plus 1 squared. So on the other side you start off with a, then you add a row and column in terms of a then add 1. The square visualization is pretty neat.
I’m sharing the work this time around because I worked on keeping my work neat. It also helped to use a bigger notebook. More room to work with. I got one question wrong due to a subtraction error.
We multiply the base an exponent number of times against the multiplicative identity, 1.
If you start with the base and then multiply by the base repeatedly, you multiply one fewer times than the exponent, and you may be confused in some cases like when the exponent is 0 or 1.
Nothing is wrong with it. It’s a square.
“perfect square” is a term defined to refer to a useful subset of squares.
What is the set of all numbers that are squares, perfect or not? What numbers are included and what aren’t? Try to figure this out.
Which one?
53
So I said that we multiply a base, let’s say 5, against itself an exponent number of times. In this case three. So we would multiply 5 against itself three times. I’m a bit confused on multiplying one fewer times than the exponent. If anything I think I could misinterpret what I said to multiply an extra time. We have 5 as a base and then I multiple three additional fives against it (which would be 54 ).
I do understand the point about multiplying it against 1. I’ve heard that point before. Thought it feels shoehorned in, just so we could have an answer for when a power is 0.
~yeah. I guess its more so: why are they called perfect/what’s the particular usefulness of these squares? Also I’m thinking of it kinda like this: 212 is a perfect square, 2.1^2 would make a similar kind of square (just 100 times smaller).
Not numbers that can be squared, right? But numbers that are considered square like 25, 100?
2.1.2) part a, you can see it on my work with an X on it.
I remember why I got it wrong. I did 144-49 in my head. For some reason my brain treated the 144 as 145. So my thought process in my head went: take 45 away first, leaving you with 100, and leaving you with 4 more to subtract, getting you to 96.
For 5^3, if you start at 5, then you multiply by 5 two times to get the final answer. You do 2 multiplications when the exponent was 3.
Yes, numbers that are the square of some other number.
If it was numbers that can be squared, that would just be all numbers. You can take any number and square it.
What numbers are squares.
Lets see:
After you square two numbers they’re always positive. So squares are always positive.
You can’t multiply up to an irrational number like pi, sqrt(2), etc.
So far negatives aren’t squares and irrational numbers aren’t squares. However, a number like 2 is a square I guess. sqrt(2) x sqrt(2) is 2. It’s a square with sides sqrt(2).
Hmm. Ok. So I think all positive integers are squares. Are decimals squares? Maybe?
21 is a square because sqrt(21)2 .
Is 2.1 a square? I guess? I can do sqrt(2.1).
Mmm. Are all positive rational numbers squares?
but then if the sqrt(2) is irrational we can still do sqrt(sqrt(2)) and then square that, giving us sqrt(2) as a square. So idk now.
Now I just have all positive real numbers as my thinking.
Am I missing something here?
Do a web search about whether pi has a square root.
Looks like it does. I looked at a few things quickly but from Gemini:
Yes, pi has a square root
, denoted as √π, which is an irrational number approximately equal to 1.772. While it cannot be expressed as a simple fraction or a finite decimal, the square root of pi exists and has significant mathematical applications, such as in the Gaussian function and probability and statistics, which describe the distribution of random events.
What is the square root of pi?
Definition: It is the number that, when multiplied by itself, equals pi (π).
Symbol: It is written as √π.
Value: √π is approximately 1.772453850905516027298167483341145182797549456122387128213.
Why is it important?
Gaussian Function:
The square root of pi is a key constant in the Gaussian (or normal) distribution function, which is fundamental to probability and statistics.
It also appears in the gamma function, which generalizes the factorial function to non-integer values.
Classical Problems:
The difficulty in constructing a square with the same area as a given circle (the squaring the circle problem) is related to constructing a length of √π using classical Euclidean tools.
Key characteristics
Irrational: Like pi, the square root of pi is an irrational number, meaning its decimal representation goes on forever without repeating.
Finite Value: Despite being irrational, it has a precise, finite value.
Woah didnt mean to copy that much. Im on my phone at work.
OK, so is that is pre-existing category, nothing new. So do you see some value in defining perfect squares now?
Mmm. I can see why they could be a category, kinda, yeah. But, like I said before, to me 212 seems the same as 2.12 . Just 2.12 produces a square 100 times smaller.
I guess my confusion on this comes from whats the point of these perfect squares?
Random(?) question:
Can area be negative? Mathematically it doesn’t seem to work out it seems, but going off the examples we covered before: holes (volume) can be negative. You have negative space to fill up. Can’t you have a negative area to fill up? Like if you were painting a wall could the unpainted wall be represented as a negative?
yeah, sure
ok instead of looking at what numbers have a perfect square, look at what numbers are a perfect square and which aren’t.
so like 1, 2, 3, 4, 5, which are perfect squares?
the perfect square concept is reasonably selective. it’s not just all numbers or all positive numbers or anything like that. making more sense now?
2.2 Higher Exponents
Do powers after 3 stop “doing stuff”? 2s makes squares, 3s make cubes, do 4/5/6/7 do anything later on?
I got almost all of the beginning of chapter problems correct. I missed 2.14) (a). I accidently did 2^3 instead of 2^2 in the parenthesis. I didn’t write it wrong. I just did it wrong in my head for whatever reason.
I got 2.24) (g) wrong. I did my order of operations wrong. I don’t think I was paying close attention. It was 5-7(25-27)^4. I evaluated that as (5-7)(25-27)^4. I think I did that because of the space I left in between 5-7 and (25-27)^4 on my paper. I think my brain than treated that as two seperate things or something. Idk.
I got the rest of the corrections correct.
Oh yeah. I did the beginning of chapter problems. I’m probably going to do them from here on out.
I think the 4th power works the same way for a 4-dimensional shape. Some advanced math deals with more than 3 spatial dimensions. Even though we can’t visualize it, we can still do math about it.
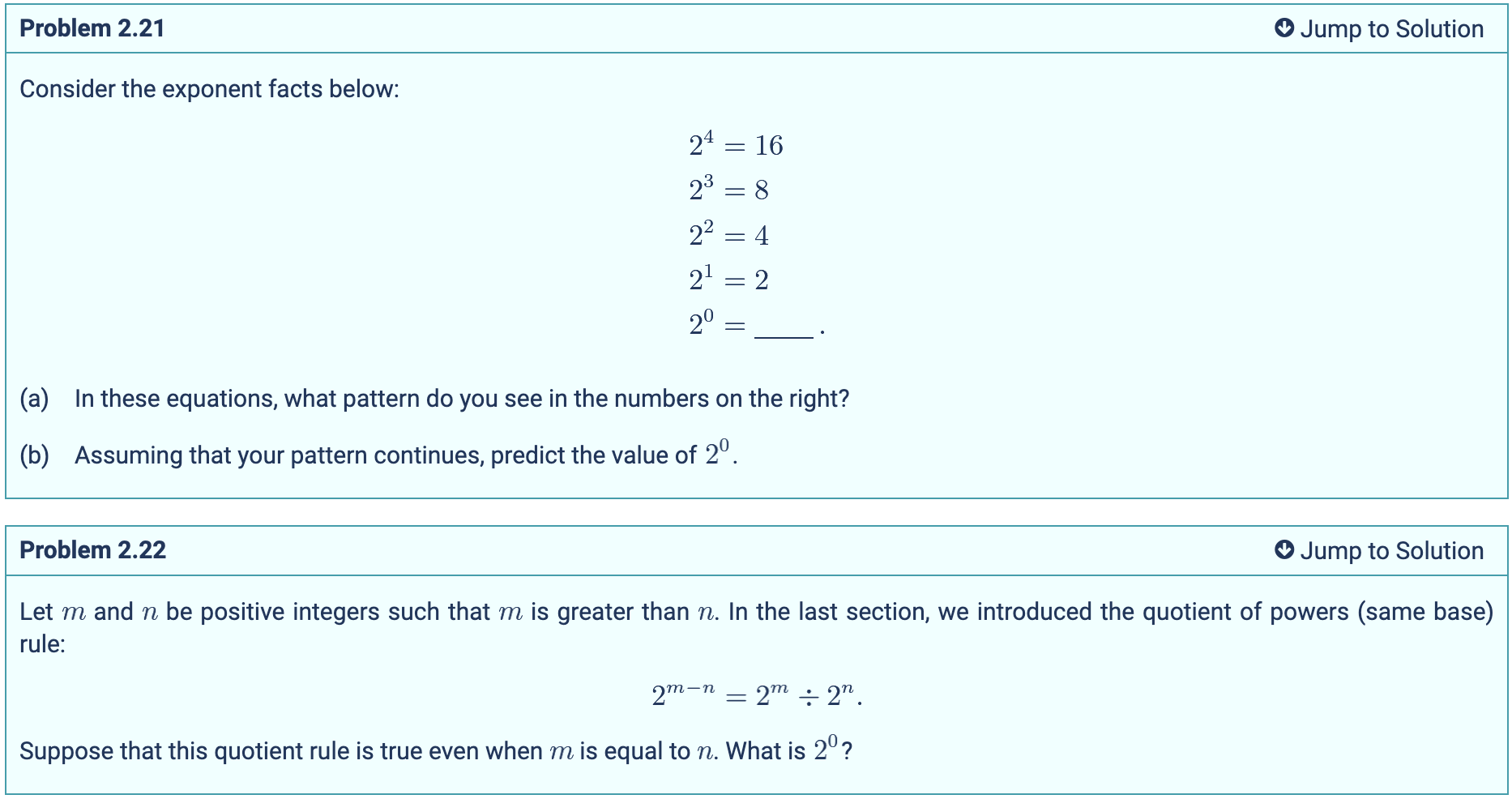
2.3 Zero as an Exponent
So the two reasons as to why we define a0 as 1 is because:
-
- We keep dividing two on the right as we decrease in exponents. So it makes sense to keep the pattern up at 20
- 2m-n = 2m / 2n , if m and n are the same then on the left side we have 20 and on the right side they divide out to 1.
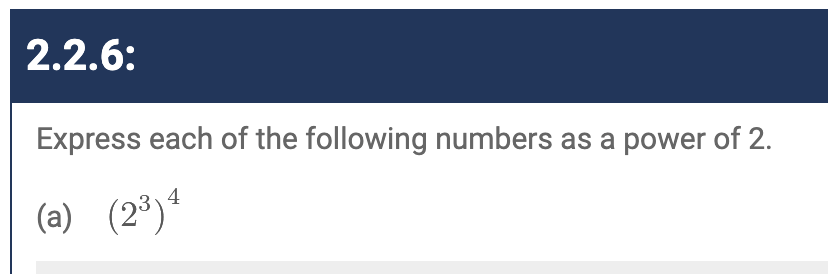
Got all these right.
Got all these right.
among those 1 and 4 is a perfect square. and something like 9, 16 would be perfect squares.
mmm. yeah i get that part. I’m more so just wonder if there’s any “higher” value here. Perfect squares are the numbers you get after squaring an integer. 1, 4, 9, 16, 25, etc. What can I get out of knowing this? Mmm. I can know that if I see 1, 4, 9, 16, etc. it has a “clean” square root. An integer square root. Anything else?