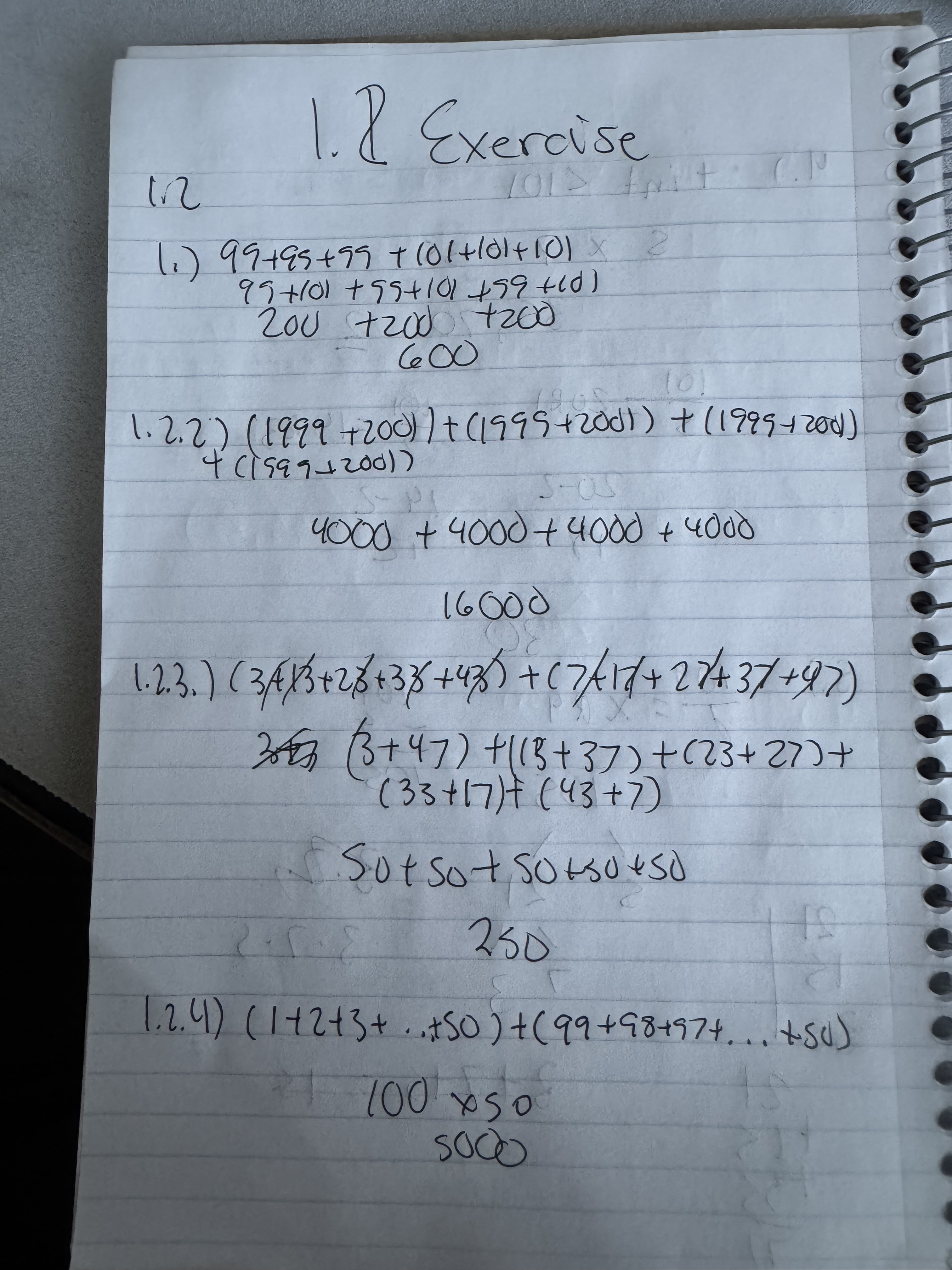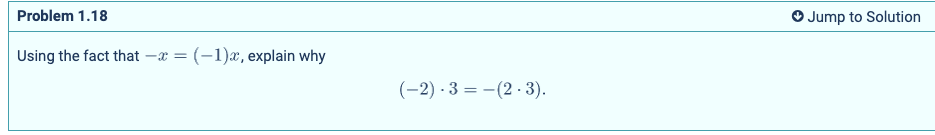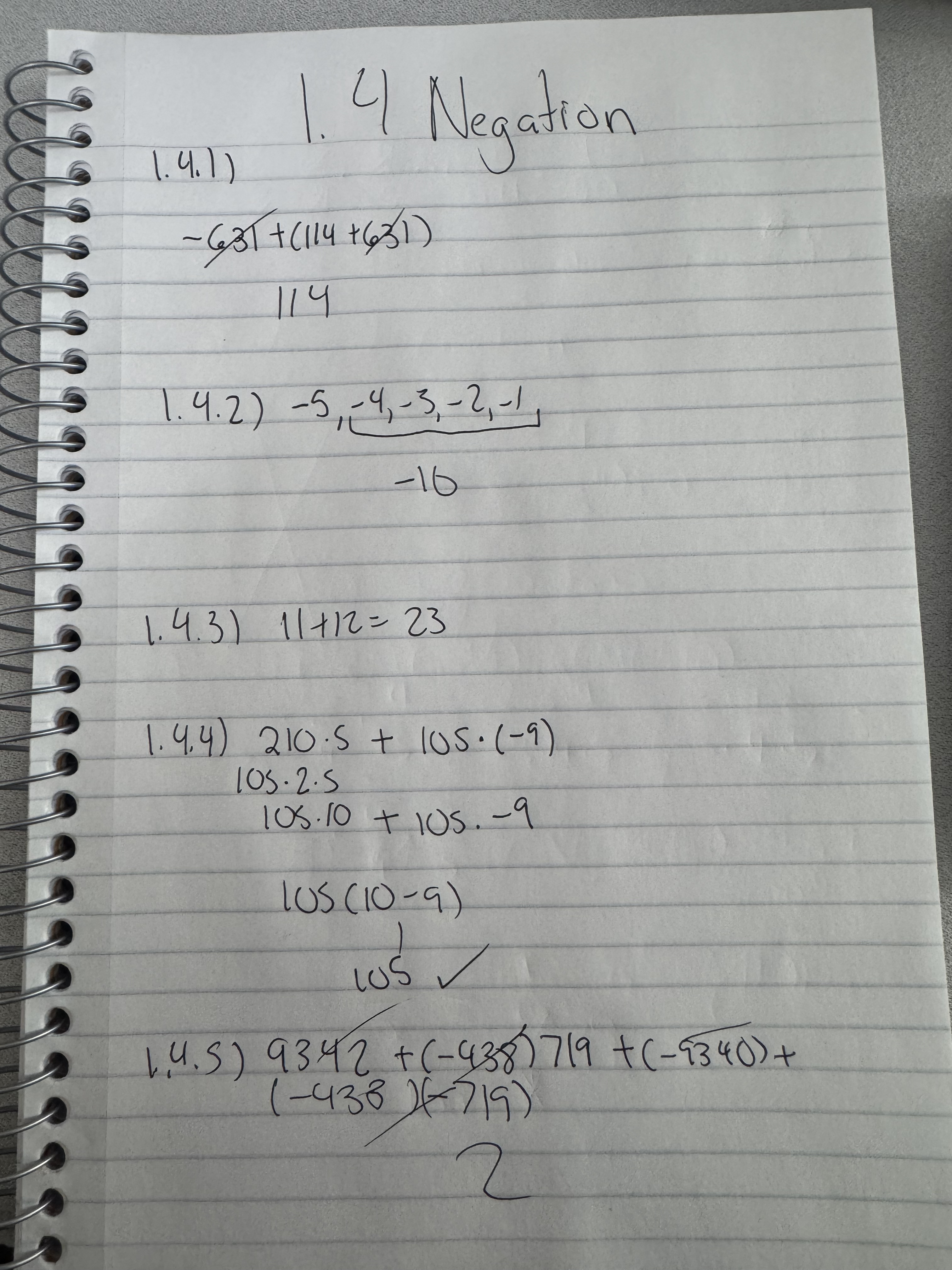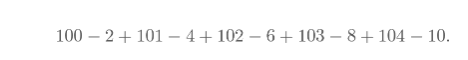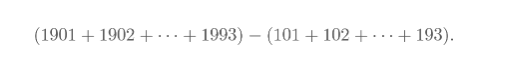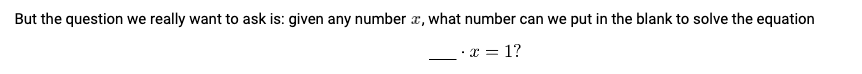Art of Problem Solving - Pre-Algebra

Other Projects
1

Project Summary

Goal

What’s your goal? Why do you have that goal? How will you judge success and failure? What bigger picture goals or values are you pursuing? How is this relevant to CF?

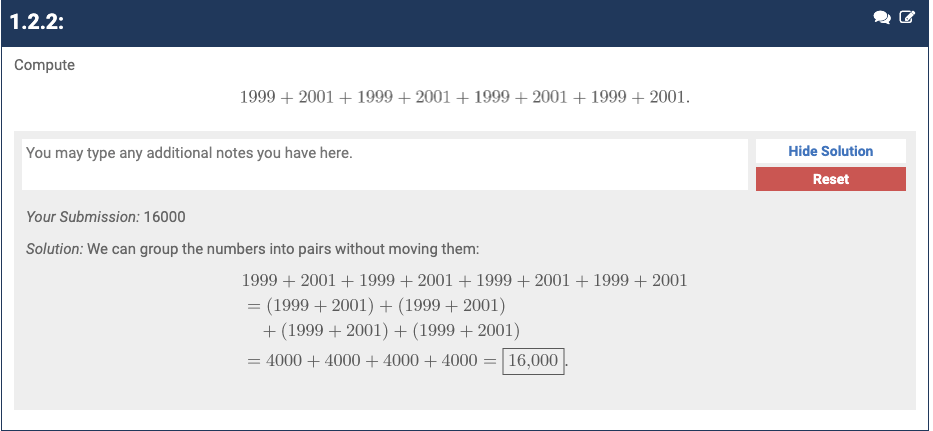
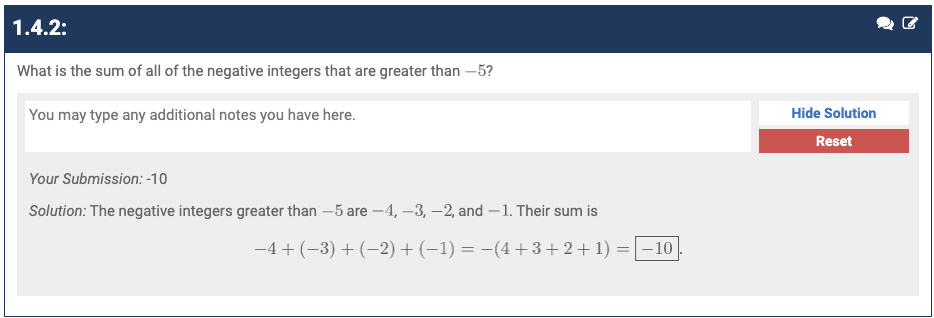
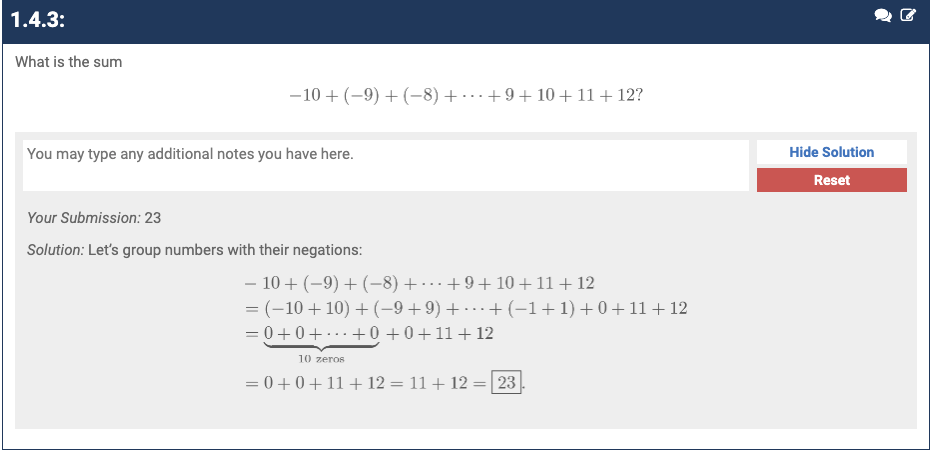
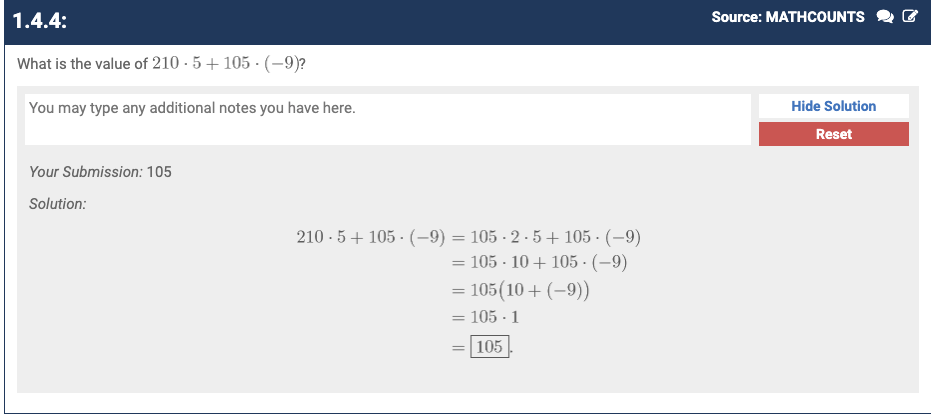
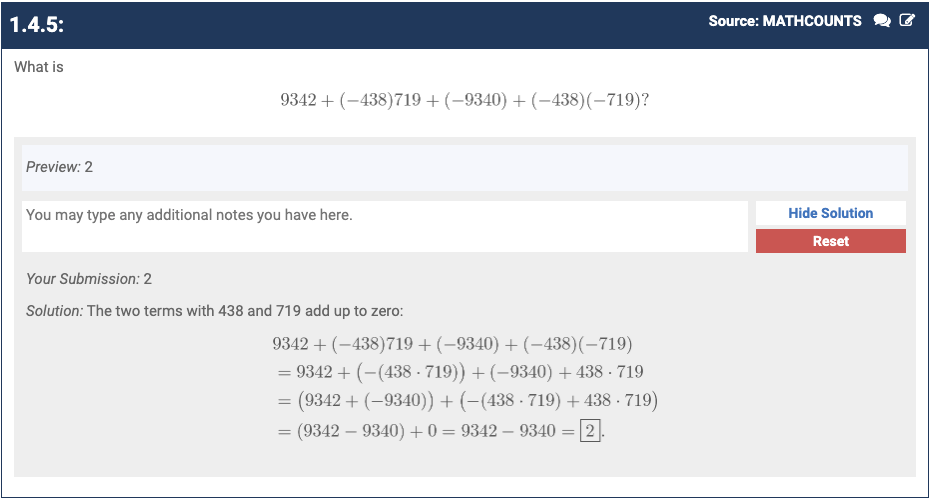
My goal is to finish Art of Problem Solving’s Pre-Algebra textbook. I want to work on some basic math stuff. I will have succeeded at this project when I have read all chapters in the textbook and completed all the problems. This is related to getting better at basic math skills for philosophy. Learning math is relevant to CF.

Plan

What’s your plan? How big is the project? What resources do you expect it to require and what have you allocated for it? How confident are you about succeeding? What sort of errors or error rate do you expect and how will you deal with that? Got any error correction mechanisms? What are the risks of not finishing the project or failing and do you have any plan to address those risks?

Spend at least 15 minutes a day with a two day buffer. I do intend to do more than that, probably an hour a day, but I just want to make the goal small. I’ve gone through a lot of this textbook before. Part of this is review and part of this is getting feedback from stuff I previously just self-studied.

I don’t know how big the project is. I don’t think its that big. I remember going through it in the past pretty quickly while feeling like I understood things okay. I don’t have any projects to compare to (of my own I mean).

I’ve finally got my schedule shortened and gotten shorter shifts on many days. So I have more time available to put towards CF.

I’m fairly confident about succeeding. I nearly finished this math textbook in the past while being a bit busier with a poorer lifestyle.

I expect some days to be too tired to do stuff. So I gave some buffer. I also made the goal short so that I will do a bit everyday and (probably) end up doing more.

On the math side of things one error I expect to run into is rushing things. Idk how to address this other than I intend to be more methodical in doing my math problems.

I’m unsure of any risks of failing this project. Mmm. I have a habit of dropping stuff like this and revisiting stuff later. I think thats a risk. Though this is only the second time I’m touching this textbook, with other stuff in my life I have re-done the basics a bunch because of dropping stuff. That seems like a waste of time. Idk how to address that risk directly. I just kinda aimed to make this a manageable project so I don’t end up dropping it. I also think finishing my latest college math class gave me some confidence.

Other People

What help are you asking from others? What value are you offering to others? Will you complete the project independently if no one else participates? Why are you sharing this with others? What sort of criticism do you want?

Feedback on some stuff I don’t understand.

Idk if there’s any value here to others (this is partially just my tutoring stuff done as a project, I thought it would be neater this way). Mmm. I think there’s some value in seeing how others learn and think about stuff.

Context

What’s the context? What’s your relevant background and track record? Why are you prioritizing this over alternative projects? Why are you doing it right now? What have you already done?’

I like math. I liked the math class (more-or-less) I just recently finished. I’m trying to build a record of doing stuff and I feel like doing something like math, which I really like, would help with that.

2

Some notes I took recently on Chapter 1.1 Why Start with Arithmetic?

Not everybody agrees on what “prealgebra” means, but we (the writers of this book) like to think of prealgebra as the bridge between arithmetic and algebra.

Hmm. I guess that makes sense, but I wonder: why is it hard (I’m assuming here) to define the math between arithmetic and algebra?

Arithmetic refers to the basics of adding, subtracting, multiplying, dividing, and (maybe) more exotic things like squares and square roots. You probably learned most of these basics already.’

Mmm. What does wikipedia say arithmetic is? From https://en.wikipedia.org/wiki/Arithmetic:

Arithmetic is an elementary branch of mathematics that deals with numerical operations like addition, subtraction, multiplication, and division. In a wider sense, it also includes exponentiation, extraction of roots, and taking logarithms.

Hmm. Idk. This feels to me as if they needed a term to denote all of “simple” mathematics. Then again I don’t really know what algebra is and how that definition would work. Idk, this just doesn’t feel well defined to me.

That toolbox is algebra. Algebra is the language of all advanced mathematics.

How all we talking? Actually all? If so, what about Algebra allows for that?

Algebra gives us tools to take our concepts from arithmetic and make them general, meaning that we can use the concepts not just for arithmetic problems, but for other sorts of problems, too.

Is this why? Instead of having 2 (3 + 5) = 2(3) + 2(5), we can instead have a (x + y) = ax + ay. Is it this variable(?) language that defines Algebra?

image
image693×196 10.8 KB

Hmm. So I don’t understand negatives and therefore 1 well. I do understand 2 and 3 I think. I do understand the fourth one too.

You’ll know all these things not because you’ve blindly applied some calculation, or because you’ve memorized some formula–instead, you’ll understand the mathematics behind all these expressions.

I remember on my first go through that not being the case for me.

Unfortunately, different mathematicians and different textbooks may use slightly different words for the same concept, in the same way that what an American calls a “truck” is called a “lorry” by people in Great Britain. So, before we go any farther, we want to make sure that we all agree on some of the words that we’re going to use.

An integer is a number without a fractional part

That includes 0. Its a number and it has no fractional part.

image

image

So an integer is a whole number/it has no fractional part. A positive number is a number greater than 0. A negative number is a number less than 0. A nonnegative number includes positives numbers and zero. A nonpositive number includes negative numbers and 0. A nonzero number is any number that is not zero or, in other words, a positive or negative number.

Oh yeah, some text will be screenshotted when copy and pasting it doesn’t go well.

3

It said you should understand that by the end of the chapter. Did you finish the chapter yet? Do you understand it yet? If you have trouble, share some of the book’s explanation about it and say what the problem is.