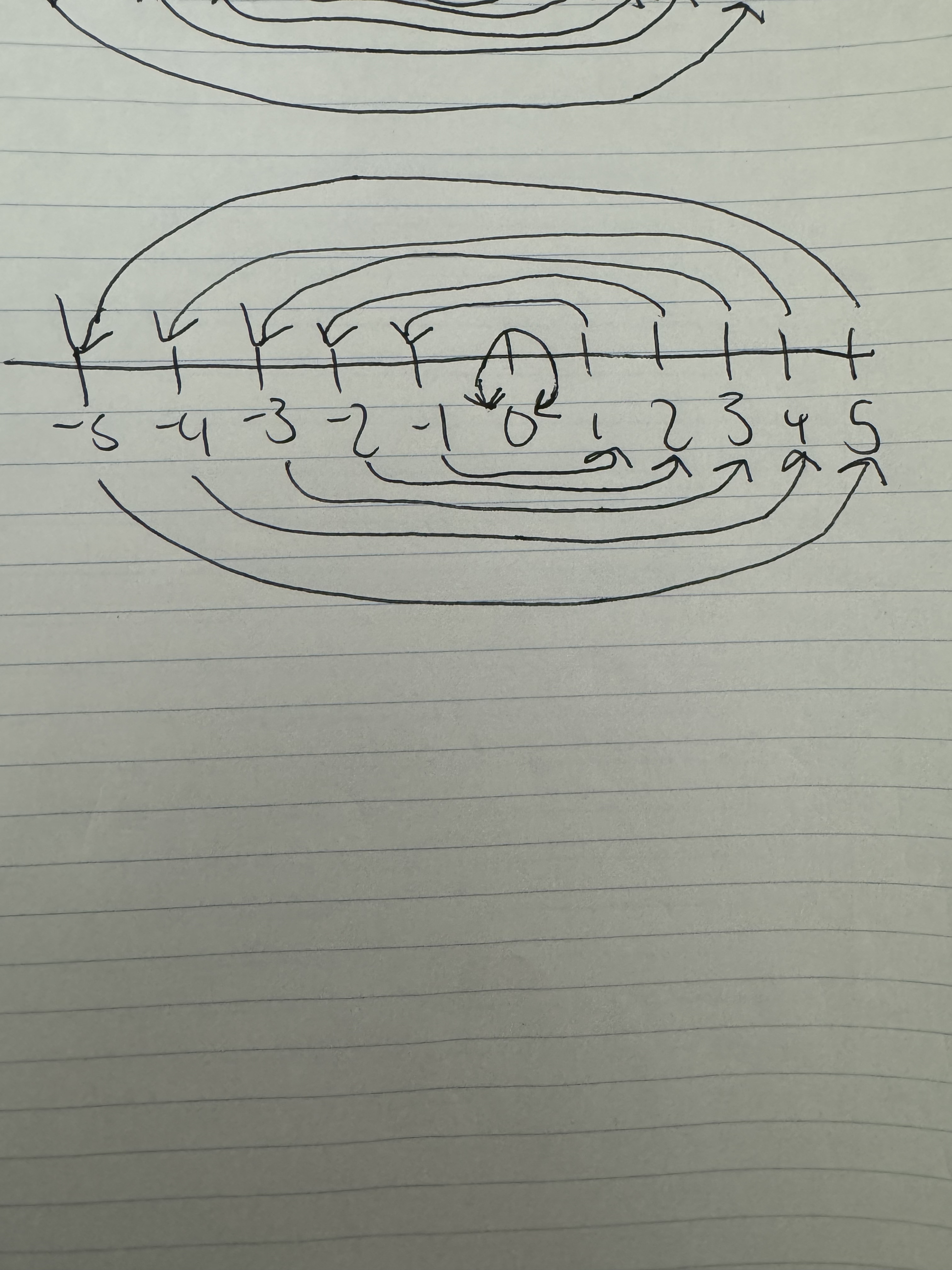
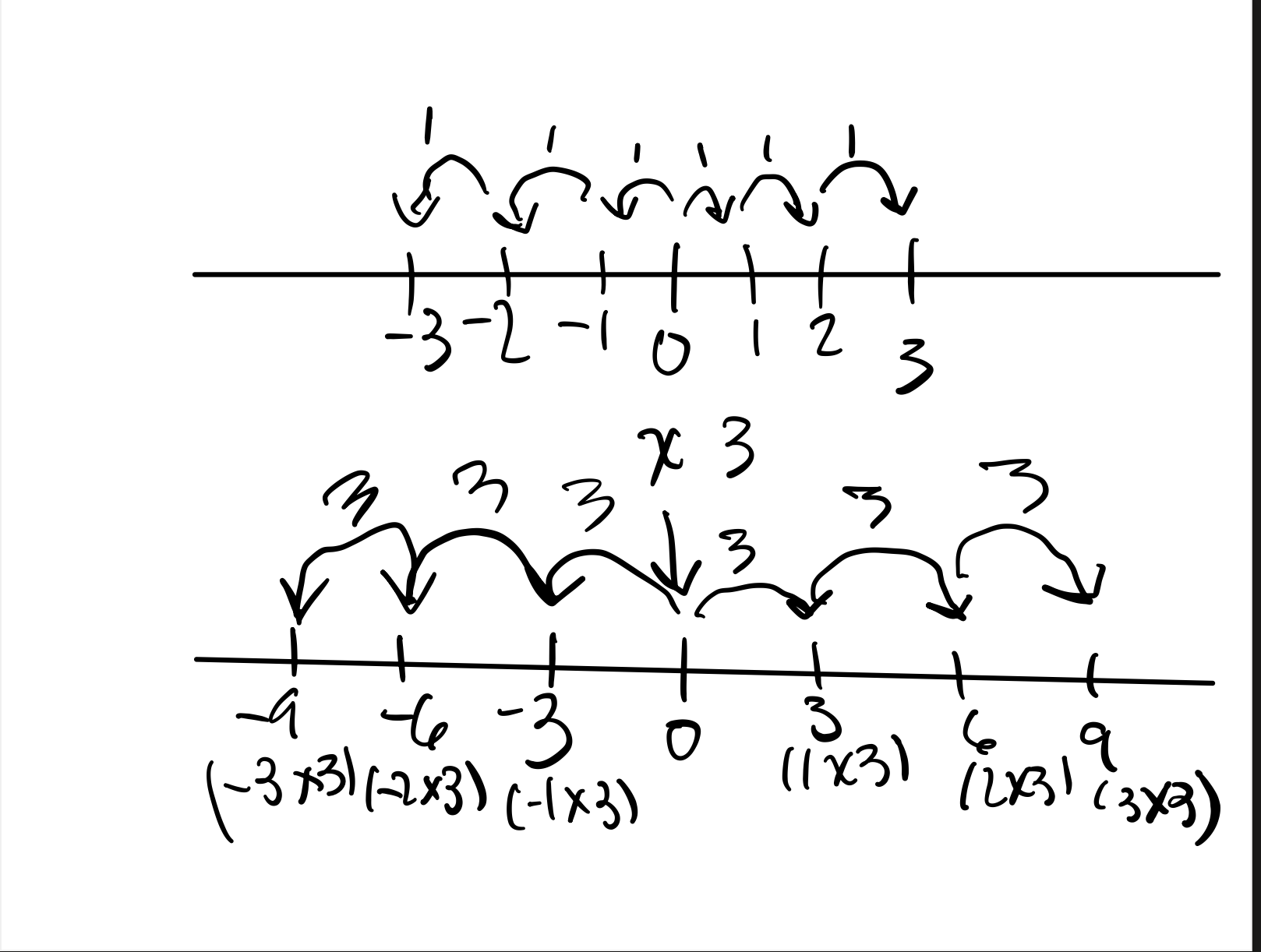
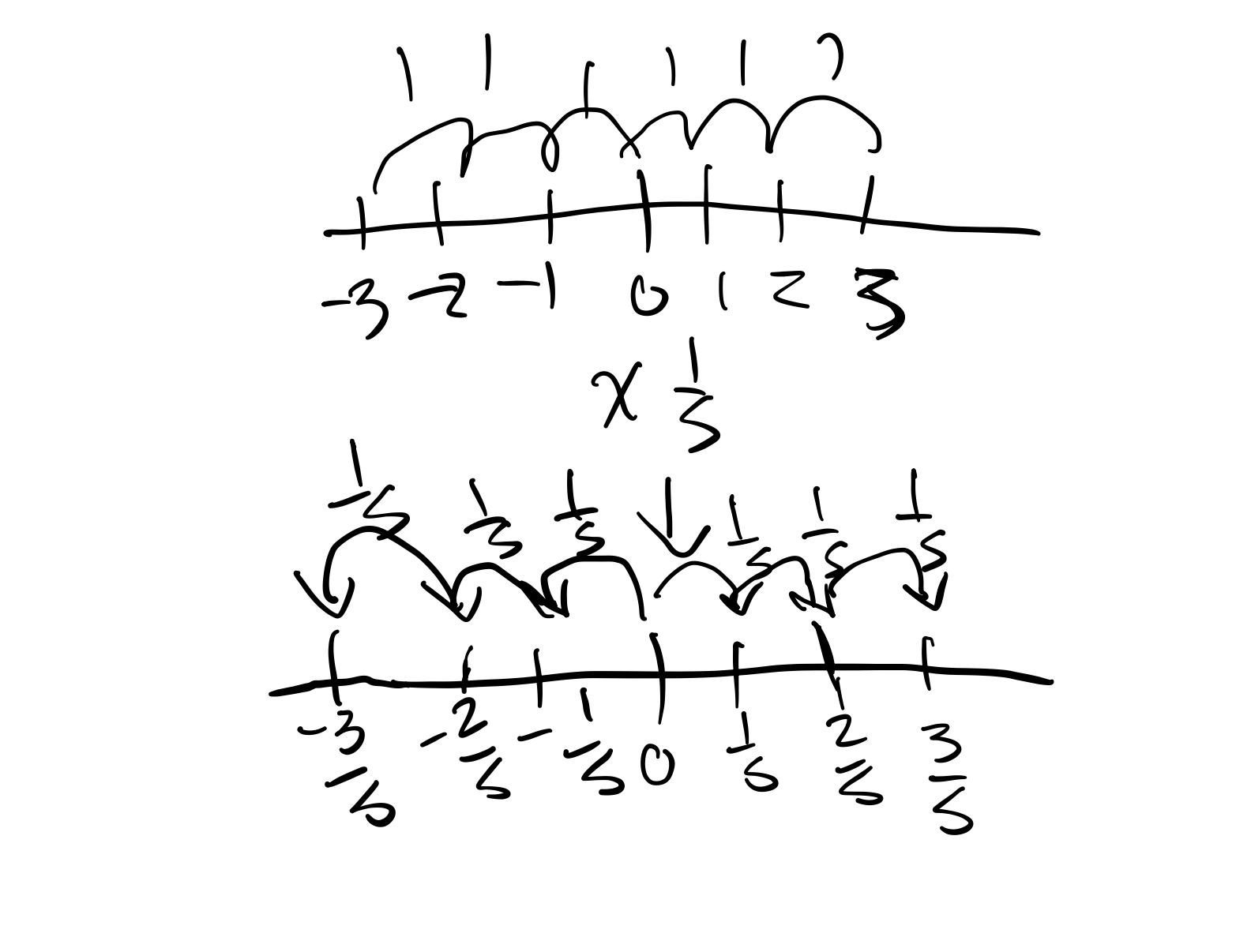
Yeah. So can you describe what you’re doing to the number line when you multiply by -1?
Reversing the order of the numbers on the number line. The 5 goes from being at the front to back as -5, -5 goes from being at the back to the front as 5, etc.
Any other ways you can think of it?
Hmmm with the lines you had me draw it looks like I’m rotating the number line 180 degrees.
Going off of the imagery of rotating the number line. If I were to add 10 to the inputs the number line would shift to the right 10(units?).
Imagine two number lines, one above the other. The top one is the inputs. The bottom one is the outputs. So you draw an arrow from 0 on the top one to 10 on the bottom one, and from 1 to 11, and so on.
Now imagine you want to change/move the bottom number line so all the arrows just go straight down. Each output lines up directly beneath the input that generates it. What would you do to the bottom number line?
Move it to the left 10
It would expand if you multiplied or shrink if you divided.
If you multiple the number line by 3, for example, the number line would be 3 times bigger. There would be a gap of 3 in-between each number.
If you divide the number line by 5, for example, the number line would be 5 times smaller. There would be a gap of 1/5 in-between each number.
OK so try defining or(x,y) with integer arithmetic. Let me know if you need more hints.
Ok. I assume that the number line stuff was to help clear up some confusions I had and then lead me into finding a solution to or(x,y). Or not, maybe you were just teaching me some stuff about how number lines work. Regardless I didn’t use the preceding information with number lines to come up with my solution.
If I’m understanding the difference between integer and real arithmetic correctly so far my solution of x+y-xy should work.
I got my solution by assuming that some of the stuff I did with logic would work directly with math. So or(x,y) = not(and(not(x),not(y)). In in-fix: !(!x&!y). Translating that to math: 1-((1-x)*(1-y)). That simplifies down to x+y -xy. Here’s the math to show that works:
x y
1 1 = 1 + 1 - (1)(1) = 2 - 1 = 1
1 0 = 1 + 0 - (1)(0) = 1 - 0 = 1
0 1 = 0 + 1 - (0)(1) = 1 - 0 = 1
0 0 = 0 + 0 - (0)(0) = 0 - 0 = 0
That is a great solution. Good job.
There are two more solutions you can find.
One is linear (no term like xx or xy) and thinking about number line transformations can help find it.
The other uses a comparison operator. One of these: > >= < <= == !=. The last two mean equality and inequality. These operators can return T or F based on whether the comparison works or not. E.g. 2 > 2 will give F. Ending with T or F instead of 1 or 0 is fine (if it wasn’t, then I’d expect the comparisons to output 1 or 0, so the solution wouldn’t change).
Sharing some writing today:
- I think today I’ll write about some self-reflection stuff.
- Recently someone called Dface on the Critical Fallibilism forum replied to an auto-generated post Elliot made for his article on procrastination. I think I’m going to read it after seeing the discussion on the article. Before I start reading it though: the thing the stood out to me about the article, and why I want to read it, is the top paragraph that got shared by the bot. It says:
- “If part of you doesn’t want to do something, then that’s a conflict that should be rationally resolved. Trying to just do it is suppressing part of yourself and is a win/lose attitude not a win/win solution.”
- I think this is a big part of my issues. While I have some issues with addictive behaviors and other bad habits. I think I’m starting to realize that a part of me, while recognizing that these habits are in some way bad, does not want to change my bad habits. Elliot in our tutoring thread mentioned how sleep is important. He gave some basic advice and then mentioned to go look up some tips myself. The thing is I have done that. Plenty of times. Yet they’ve failed a bunch of times. Now while I do think I should look into resources dealing with addictive behavior and stuff, I think there’s a large part of me that is fine with how I am now and is ok with how I am now. When I recently re-listened to the audiobook of Unfu*k Yourself he made a good point about how people are actually, in a certain sense, ok with how their life is. The point went kind of like, “If how your life is actually did bother you completely, you would have done something about it. Your ok with how your life is in some manner for you to not be doing anything.”
- When I think about some of the simple tips Elliot shared such as:
- “One is: don’t do things in bed other than sleep. If you aren’t going to sleep yet, don’t get in bed.”
- I’ve realized that part of me doesn’t want to fix my sleep schedule. Or, more precisely, their are certain things about my bad sleep habits that I like. Doing stuff right before bed feels like unrestricted free time to me. I can watch a video, read manga, read novels, play some games, at least for a little bit because I’m in bed. Maybe this is a remnant from when I was younger? I have control over my time (compared to when I was younger) before bed to not need to do this. Their could be other stuff but that’s a start.
- I think a part of me is hostile to getting my life together. I’ve noticed this in other aspects of my life. I know part of the reason why I’ve had issues getting started on dating is because I view becoming attractive/people who date as idiots in some manner. I’m hostile towards putting effort into becoming more attractive not because I think being attractive and dating is a waste of time (those are rationalizations on my part), but because becoming hot = becoming stupid. Or a better way to put it, I’ve equated being unattractive (or at least viewing myself as unattractive) as the same as being smart in some manner.
- Hmm. Out of time for now. I’ll come back to this later, but I wouldn’t be surprised if I thought about it some more and made some bad associations like, “Geniuses live messy lives. So I should live a messy life.”
I’ve thought about this a bit more and while I think I’m understanding the number line transformations more, I’m confused on how number lines would work with two different inputs.
How do I put on a number line x + y? Unless there’s some solution using only x or only y.
I haven’t started working on the comparison operator one yet.
In order to use the number line with 2 inputs, combine them first. The most straightforward ways to do that are adding or multiplying them.
Well multiplying them would give me a term like xy. I’m looking for a linear solution. So adding them. Would result in just x + y. So when you say combine them first, do you mean turn them into one term? I can’t do that without multiplying, but then it wouldn’t be linear. So we have x + y. I’m still confused on how to put this on a number line. Would I create a number line for each version of y? Since I’m only concerned when y = 0 and when y = 1. Or would I do this on the x y plane? Is that a type of number line?
For the comparison one I got. x + y > 0. Is that fine?
0 + 0 > 0, 0 > 0, false
1 + 0 > 0, 1 > 0, true
0 + 1 > 0 , 1 > 0 , true
1 + 1 > 0, 2> 0 , true
The sum x+y is 0, 1 or 2.
You know the goal for what you want to transform it to in each case:
0 → 0
1 → 1
2 → 1
If you think about it with two number lines, the left numbers correspond to the top number line and the right numbers to the bottom one.
What mathematical operation could help here? What conceptually do you need to do?
Correct.