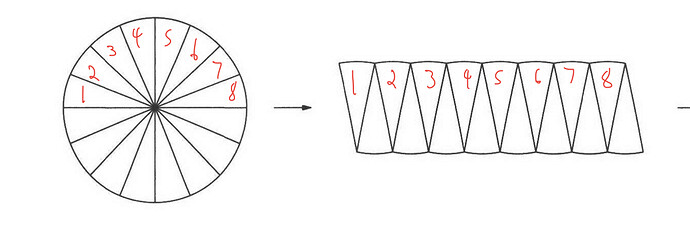
I posted about an algebra word problem on my blog
I’m skeptical about the yellow highlighted part. My intuition is that the “length” of the “rectangle” should be maybe a bit more than half the circumference. I haven’t been able to figure out a great explanation why I think that though, might try again later
Have you tried to go through it step by step and see what is happening?
What do you think of the sentence before the highlighted sentence?
I hadn’t really, but after reading your question and thinking about it more, I think maybe I got it. Gonna write my thoughts up.
I think I was only looking at like one half of the sectors or only thinking about one half or something.
Like I imagined taking the top half of the the circle sectors and spreading them out:
And I was thinking “well now they’re more spread out than they were in the circle, and have like a big angle between them, so the resulting shape we created by spreading them out should be longer.”
But the space between the sectors is sized for accommodating the sectors from the other half of the circle, which are part of the original circle, so my thought doesn’t actually make much sense.
It seemed to make sense to me but I think I was tunnel-visioning on one “half” of the circle (as explained above) so I guess I didn’t fully understand it.
Ok, this gives a better idea of what you think.
Your thought doesn’t make sense, but this isn’t the reason why.
Like, you could also take all the triangles and put them all out into one long line (instead of making them into a rectangle). In that case, they would still be “spread out” in the same way, but not to accommodate any other part of the circle. Do you understand what I mean?
I think so. And I guess in that case, based on what the book says, the length of the line would be equal to the circumference of the circle?
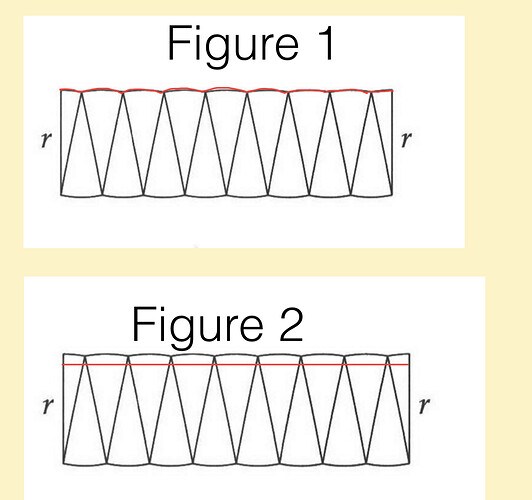
Hmm wait a second. I think part of what was bothering me was that the sectors have a curved part but then we’re re-arranging them into a rectangular shape. With a “normal” rectangle, you can multiply the length times the width to get the area. You can also add up 2L + 2W to get the perimeter. With this example from the book with the rectangle made out of circles, though, it seems like things would be a bit different. Like, when we speak of the “length”, I think I have an intuition that we’re not talking about like, the measurement of a line that’s following the slight curvature of edge of the sectors across the rectangle. Instead I’m imagining a “length” line cutting across the rectangle. Here I’ll do a drawing to make this clearer so it’s not just in my head:
“I’m imagining a “length” line cutting across the rectangle” corresponds to figure 2.
OTOH maybe that intuition is wrong. Another relevant thing: if you follow the curve along the edge of a sector and continue on towards another sector, it seems like you could get the same measurement, regardless of the angle between them. I made a figure for that. The green represents (poorly drawn) sectors and the red line represents tracing a line along the edge:
I don’t have a conclusion here yet…just some thoughts.
Yes.
But since you are saying “based on what the book says” I assume you still don’t really understand why.
(Edit: I realized after finishing the post that maybe what you aren’t sure about is the approximation part: if you draw a straight line, not following the arc/curves, then it isn’t going to be exactly equal to the circumference of the circle.)
Right. It’s just meant to be an approximation, to give you an intuition for why the formula works.
In the case of your lines in figure 1 (the curved line) vs figure 2 (the straight line), which one would be longer?
1 Like
And you can imagine dividing the circle into more sections which makes the approximation better.
1 Like
I definitely wasn’t sure about that! Yesterday, after rereading the material I pasted, especially the second to last sentence in the final paragraph (the one that starts “This isn’t a completely accurate explanation…”) I realized that it probably wouldn’t be exactly equal to the circumference and that that’s what they were getting at.
The curved line in Figure 1 would be longer cuz it’s curving up and down instead of just going straight.
Right, ok, so can you connect that back to your original problem with the explanation?
Like, now you are saying that the straight-line length would be shorter than the curved line.
But originally, you thought that the length of the “rectangle” would be a bit longer than the circumference.
Do you think these two things contradict? Or do you think they are talking about different things?
I think I thought the “rectangle” would be longer partially because the angle between the sectors was “spreading things out” a bit somehow.
Separately, I think I wanted to use the curved line as the “length” of the “rectangle” somehow, and hadn’t quite worked out how to do that or what the implications were.
I think as you put my view (which is a fine way to put it, and things were super unclear in my own head so I don’t object) there is a contradiction. The length of the “rectangle” being a bit longer than the circumference would make sense if putting the circle in a “rectangle” somehow overstated the dimensions of the circle. But if the straight line (Figure 2) “length” of the rectangle is shorter than the curved line, that would indicate that, if anything, rectangularizing the circle understates the dimensions of the circle, and that if you multiply the “length” times the “width” of the “rectangle” you’ll come up with an area that’s a bit short of the circle.
I’m not sure from this where you are with the problem, what your current theory is, if you understand it any better, etc. (If you are still having trouble, there are more things I could say, but it is hard to figure out which things to say without having a more clear idea of what your current understanding is.)
I think it makes sense to me that the “length” of the rectangle is approximately half the circumference of the circle, and the “width” is r, and multiplying the two gives us an approximation of the area.
In fact, the “length” of the “rectangle” is a bit shorter than half the circumference, because the “length” of the “rectangle” is just a straight line while the circumference is a curving line that, in our “rectangle”, curves up and down. But as an approximation, this stuff is okay.
Right, this is correct.
Do you see the mistake you were making earlier? You originally had the opposite intuition, and thought maybe the rectangle length was longer than half the circumference.
Yeah. I think I was thinking about something like the curved line from Figure 1 as the length, and then was ALSO worried about the “angle” between the sectors causing a problem. So maybe I thought that like, maybe the baseline was that the rectangle length should be equal to half the circumference, and then there was this other factor that would make it greater than half. It was a pretty confused thought process.