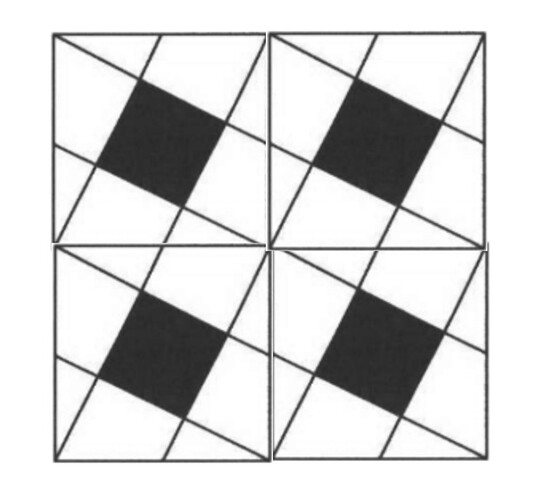
I initially took their hint as meaning to extend lines outside the square. That’s a common technique. I quickly got a solution by looking at it that way:
Maybe you can figure out a solution from this pic.
But I don’t think this is the intended solution. I think the hint meant to try to calculate the area outside the black box – the white area.