Justin, it seems like maybe you’re waiting for me to prompt you more instead of doing the second part?
No, I had a bigger misunderstanding than that, actually. I actually thought you were describing the general method there, of like how to approach these kinda problems or something, not suggesting that I go through all the steps now. So my initial reaction was like, confusion and surprise at you bringing this up (not mad at you or anything, mind you - but am kind of annoyed at myself for misunderstanding/misreading).
You should solve this problem in like 5 different ways and try to understand it. You need to go deep instead of moving on and not fully understanding some other problems.
I agree. I was starting to look at the other solutions people suggested and am planning to go through them and write things up. But I think I was prematurely “done” with your approach or something, idk.
In my earlier solution, I set the formulas for the center big diagonal square and one of the big diagonal squares equal to each other, and from that I got T + P = S, and I used that to get the answer.
If we look at Elliot’s image and see that the black squares and the small triangle + trapezoid little squares are the same size, then we can just say that T + P = S directly, without having to figure that out in terms of algebra on the bigger squares. Then we can use that information in the equation for our original square as before and solve the problem:
I. Equality of Black square and other small squares: T + P = S.
II. Original square: S + 4P + 4T = 400
Substitution of I into II: S + 4S = 400
5S = 400
S = 80.
The image Elliot made is very helpful to see this solution because there are no “whole” squares EDIT: (other than the black square, but I had in mind the little triangle + trapezoid squares here) in the original image (though, reflecting back on it, I did imagine “turning” e.g. the small triangle with side FC around so that it would “complete” the trapezoid with side EC. Maybe my not mentioning this or thinking this through more was more suppression)
Yes.
Now can you look at what that means in terms of shapes and pictures? Try to connect the numbers back to the things they refer to or model (the shapes). I was able to do basically the equivalent of that solution but without actually using algebra. It’s actually pretty simple and intuitive if you figure out how to think about it and what it means.
EDIT: Quoting math apparently glitches out, but I’ll just leave it because I don’t know an easy fix and it’s still legible enough to figure out what I was trying to quote if you look at Justin’s post.
Yeah. I was trying to figure out what was going on earlier. Like did you totally miss that or were you suppressing it?
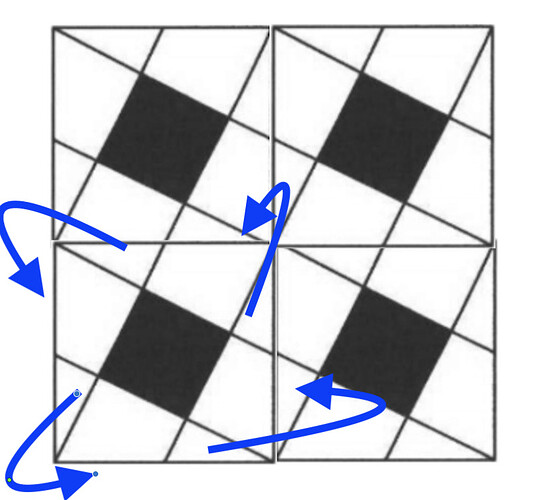
When I looked at my expanded picture, basically the first thing I noticed was a (tilted) tiling of small black and white squares, and that the white squares were the same size as the black squares. And since the white squares consisted of T+P that was actually useful information that meant a black square had the same area as T+P.
What comes to mind is the thing I said above:
(though, reflecting back on it, I did imagine “turning” e.g. the small triangle with side FC around so that it would “complete” the trapezoid with side EC. Maybe my not mentioning this or thinking this through more was more suppression)
An image to show what I mean (I’m trying to show the small triangles from the original square getting rotated around to “complete” their trapezoids, so that the original square becomes a “cross” of 5 squares):
So with that approach you’d have 5 squares of the same size, which you knew had a total area of 400, and you could just divide the area by the 5 squares to get the area of one square (such as the shaded).
I didn’t complete this thought initially, but it was probably like one of the first things I thought of.
Yes. So the original square has the same amount of stuff as 4 white squares plus a black square. Which is the same area as 5 black squares. So you divide the total area by 5 and get the answer without really needing an equation. Make sense?
Yep! Sorry that took like 2 days lol
Why didn’t you complete it?
Was this one of the things you dismissed as being “too easy”?
maybe? or like, it seemed not rigorous enough, or something? but anyways it was a lead I should have followed, even if I wanted to prove it to myself more thoroughly later…
One method change I can make when trying to figure something out is to try writing down every single lead or thought that’s coherent enough to write down, regardless of how incomplete it might be and regardless of any other issues I might have with it. Maybe that’ll help with the suppression some…
Ignoring it because it’s not rigorous enough seems the same as ignoring it because it’s too easy.
Do you see that rearranging is unnecessary? You can just count T’s and P’s and know each pair of them is the same area as a black square. Or you can see that the T+P triangles have the same area as a black square and count those.
Though I guess you mean something more like – it seemed to be based on sight/visual alone, so wasn’t necessarily correct?
I still don’t understand why you thought that it wasn’t OK to say that the black & white squares were equal, and the white squares were made up of a trapezoid and a small triangle, but it was OK to call the 2x2 squares “squares”.
Just to be clear – this is friendly, and I’m not trying to pursue meta discussion that you aren’t interested in. I am bringing this stuff up because I think that you blocking brainstorming, possible solutions, etc, for being “too easy” or being the wrong type of idea is directly relevant to the problem you had finding a solution to this question.
Interestingly, if you expand for the whole context, the Latex is fine. So the glitch seems to affect selective quotes specifically?
Yeah.
I think suppressing.
I misunderstood what you were asking for above.
In my mind, the formulas I wrote already covered this, so I thought maybe you were asking to think up a different angle on the problem that was visual and connected somehow with the stuff we figured out. I now think you were just asking to apply the idea or thought behind the formulas directly to the picture or something, instead of doing things algebraically.
Right.