A simpler problem, which you should be able to analyze and solve in several different ways, is 2+3.
I went back to the start of the book and tried going through the first substantive subchapter and wrote it up in Ulysses, similar to what I did for Simply Scheme.
I think maybe doing something like that for all the material in the book would be useful for getting a better handle on the material.
Iām not sure I can/should publish it though, for copyright reasons. Maybe Iāll just share little bits about parts I have particular trouble with.
I decided that, since my ghost website has membership functionality, I could address my concerns somewhat by making my math stuff a members-only post (membership is free)
Another post.
Did you go through the entire chapter you were working on for the last problem (chapter 11), and do all of the other questions in it?
I canāt tell from this if you mean that you started at the geometry part of the book (so maybe chapter 10?) and did everything from that point, or that you have just been skipping around.
Yes.
I started from chapter 9 on this latest pass through.
Ok. There were some other ratio problems in Chapter 11 that are relevant to what I was talking about, re using ratios to solve the problem you were working on.
Edit: to be clear, they are not the same type of problem, but they use some of the concepts needed.
1 Like
Also, some of the angle rules in chapter 10 are relevant to the problem.
1 Like
So the original thing I said was:
Looking through the book you are using, I think they didnāt actually cover similar triangles at all.
I assumed you were familiar with them (especially since you know about special triangles, e.g. the 30-60-90 triangle).
But maybe the issue you are having with understanding the way I was thinking about things is that you donāt know what I mean by similar triangles. That is how I solved the original problem, and also how I would have found the height of the right triangle (line OF, which you created when you drew some extra lines), which I was talking about here:
I just looked at those problems again, and the ones I found used either circles or squares, which are all similar with each other. (All circles are similar to each other, and all squares are similar to each other.) I didnāt find any that used triangles, and I donāt think the concept of similar triangles is covered at all.
So, the problems I was talking about use the ratio concepts needed. But they donāt actually cover the triangle concepts - e.g., that triangles can also have similarity, just like squares or circles, so you can also use ratios with them.
Yes
Ok. That material seems familiar to me, even if itās not in the current book
Does that help? Did you already know what I meant when I said similar triangles and ratios?
Iām just not sure if you have enough info now to have a better idea of what I meant & try to look at the problems again (finding OF as a stand alone problem, and also the bigger problem of finding the area in the original), or if you mean that you already knew this, so it wasnāt new/helpful information.
To be clearer about this: special triangles are just a special case of similar triangles.
lemme look at it again
We know \overline{GD} is 10, that O is the midpoint of \overline{GC}, that \overline{OC} is 5\sqrt{5}. We know that \triangle GDC and \triangle OFC share \angle C, and that both triangles are right triangles. Since theyāre right triangles that share another angle, they must have the same angles in their third angle as well. So based on all that (having the same value for all 3 angles, having hypotenuses where the bigger triangleās hypotenuse is 2x the smaller oneās) we can say that theyāre similar triangles where \triangle GDC is a 2X scaled up version of \triangle OFC. Since \overline{GD} is 10, this would mean that \overline{OF} is 5.
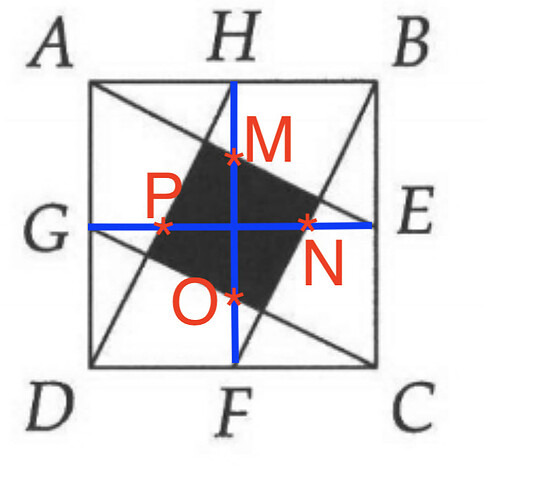
Yes.
And you could have done the same thing without using the measures of GC and OC (which you also found through pythagorean theorem).
We know that \triangle GDC and \triangle OFC share \angle C, and that both triangles are right triangles. Since theyāre right triangles that share another angle, they must have the same angles in their third angle as well. So based on having the same value for all 3 angles we can say that theyāre similar triangles where \triangle GDC is a scaled up version of \triangle OFC.
\overline{GC} is a diagonal running directly from point G to point C. (This next step makes sense to me but Iām not sure what like math rule it is). Point O, which is the midpoint of \overline{GC}, is also thus halfway between \overline{GE} and \overline{DC}.
\overline{GD}, which extends the full distance between \overline{GE} and \overline{DC}, is 10. So a line extending half of the distance between \overline{GE} and \overline{DC} - that is to say, \overline{OF} - is 5.
I meant something simpler.
You could start by just writing out what you know about the triangles already, from the information you were given in the problem.
The fact that you can figure out more than one way to look at the problem is good.
But you seem to overlook the simpler solutions. Itās not just once or twice that it has happened: it seems to happen repeatedly. I know this was talked about earlier, as something you actually were doing intentionally: you were trying to respect the difficulty of the problem, so you were looking for a difficult solution.
I think there is something going on here, but Iām not entirely sure the best way to help.
One thing you could do is actually try Elliotās suggestion of finding & explaining multiple ways of doing a simple problem, like 2+3.
Another thing you could do is after you have finished a problem, go back and try to do it other ways. And then try to figure out the most direct route to the answer, the easiest route to the answer, etc.