LMD Async Tutoring

[LMD]

@Elliot

Do you like this one better?

or(not(and(x, y)), not(and(x, y)))

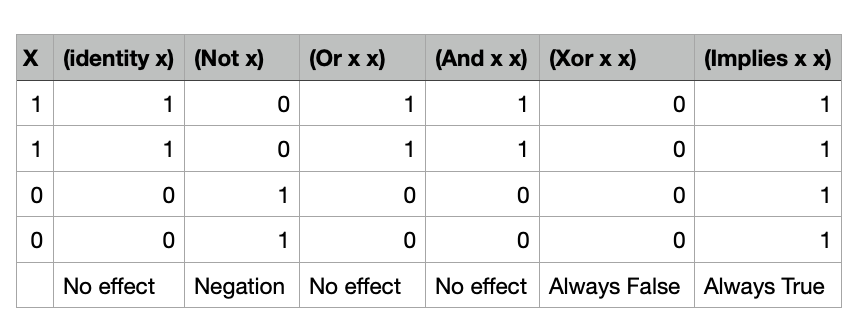
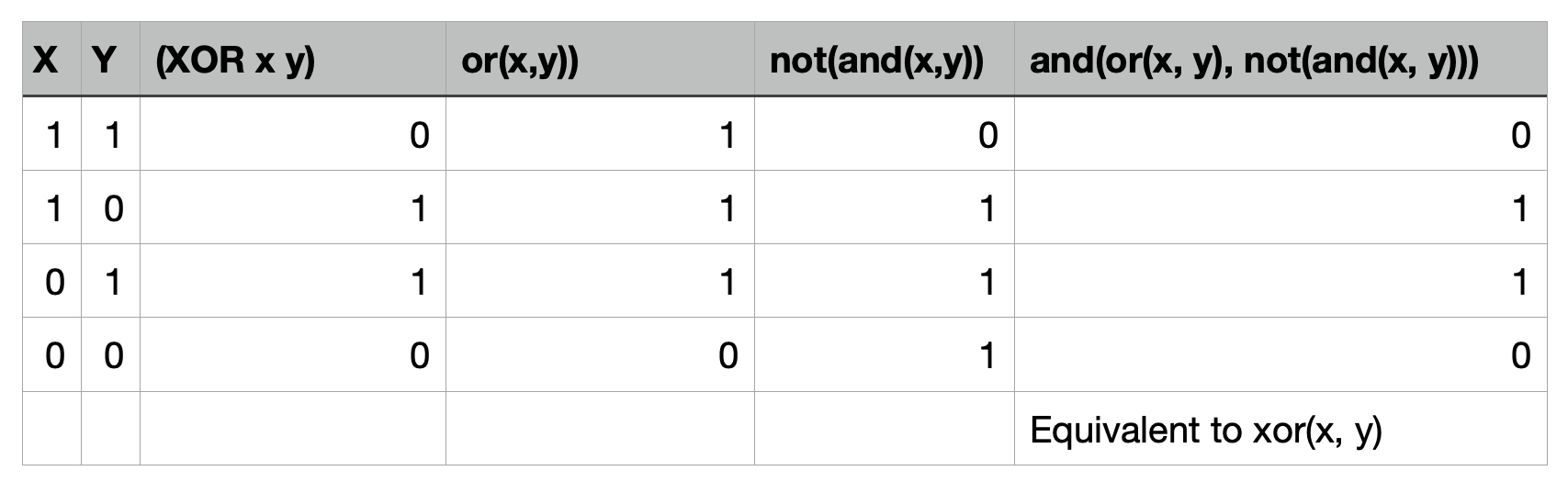
No. That’s interesting how that contains not(and(x, y). And interesting how when you ‘or’ something with itself you get the same result. So the or operation is not doing anything to the not(and(x, y).

[LMD]

Oh interesting. The same thing happens with ‘and’ (the same result). And xor and xnor make all outputs 0 or 1 respectively.

[LMD]

Okay cool I see Eternity realised that at the same time too. I’ll continue through their thread. I made part of this assignment table already on my own.

Assignment from Eternity thread:

@Elliot

Make a truth table with the following columns (I’ll use s-expression notation this time to emphasize that content and notation are independent):

x
(identity x)
(not x)
(or x x)
(and x x)
(xor x x)
(implies x x)

I haven’t encountered the ‘identity’ operation yet but I am guessing it just outputs the input.

Oh lol I just realised that I didn’t need four rows because there are only two values of x.

[LMD]

@Elliot

They don’t have any more information available than when receiving 1 input, so they actually have to give the same outputs as one of the functions that takes only 1 input. There are only 4 binary functions of 1 input: one, zero, not, identity which correspond to the 4 possible truth tables for a function with 1 input (10, 11, 00, 01 are the only 4 options). (The one and zero functions don’t actually need any input because the output is the same regardless of the input.)

Make sense?

Oh this is so cool.

[LMD]

Next assignment from Eternity’s thread.

@Elliot

Next you can try to reinvent De Morgan’s two laws. They’re for converting between “and” and “or”.

Law 1:

or(x,y) = ?

Answer only using: and, not

Law 2

and(x,y) = ?

Answer only using: or, not

Max 60min.

Here are my notes (I also made a series of truth tables/tables. Though they probably don’t make much sense, I thought I’d share.)

Alright. What do I know?

nand(x, y) = not(and(x, y))

AND and OR give the same output when both inputs are identical.

AND and OR give an opposite output when the inputs are different. Under those conditions OR is 1, and AND is 0.

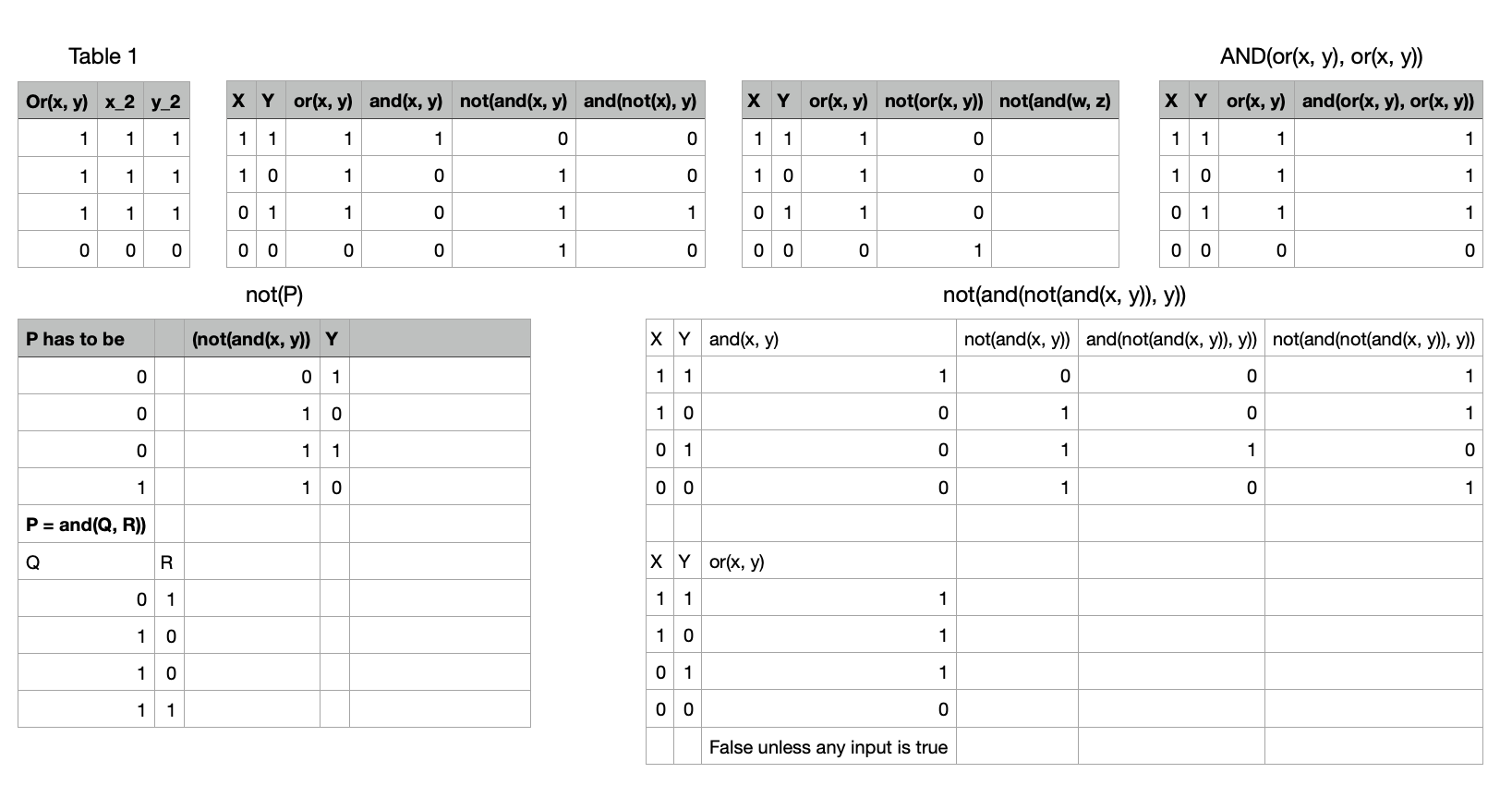
or(x, y) can be converted to and(z) using only AND, NOT. ← wait thats not necessarily the case.

Okay lets work backwards. What inputs to an AND gate will give the same output as or(x, y)?

What inputs to NOT will give the same outputs as or(x, y)? 0, 0, 0, 1.

Okay, stuck on law 1. 12 mins to go. Maybe I’ll try law 2.

Give up with 6mins left.

---

Hmm okay, I’m giving up. I’m not going to make this in time. I think I’m getting myself a little confused. One thing I tried to work backwards from some hypothetical expression NOT(P) and asked, what would P have to be for NOT(P) to equal or(x, y), if P can only be expressed with x, y, not, and.

I’m going to not read ahead on the Eternity thread in case you have any feedback particular to my attempt.

[Elliot]

You can read further.

[LMD]

Okay, moving on to the next assignment:

@Elliot

I don’t think most people ever reinvent the laws. I thought it was worth a try. Let’s try this next (there’s a chance it’s too hard but you did the same thing with nand so worth a try):

It turns out that {and, or, not} is a universal set of logic operators (this is closely related to stuff you may have heard about computational universality). You can construct all the other operators from them.

Assignment: Using {and, or, not}, construct xor, nor, implies and equality.

Max 60min.

PS This is standard logic. There are other types of logic (that you don’t need to know about) including reversible logic, where, given the outputs and the arrangement of operators used, you can figure out what the inputs were. Reversible logic is relevant to quantum computing and to computing with low energy usage.

Assignment: Using {and, or, not}, construct xor, nor, implies and equality.

My working:

nor is just not(or)

xor is true if the inputs are different, and false if they’re the same.

identity is true if the inputs are same, and false if they’re different.

right so not(xor) = identity and not(identity) = xor

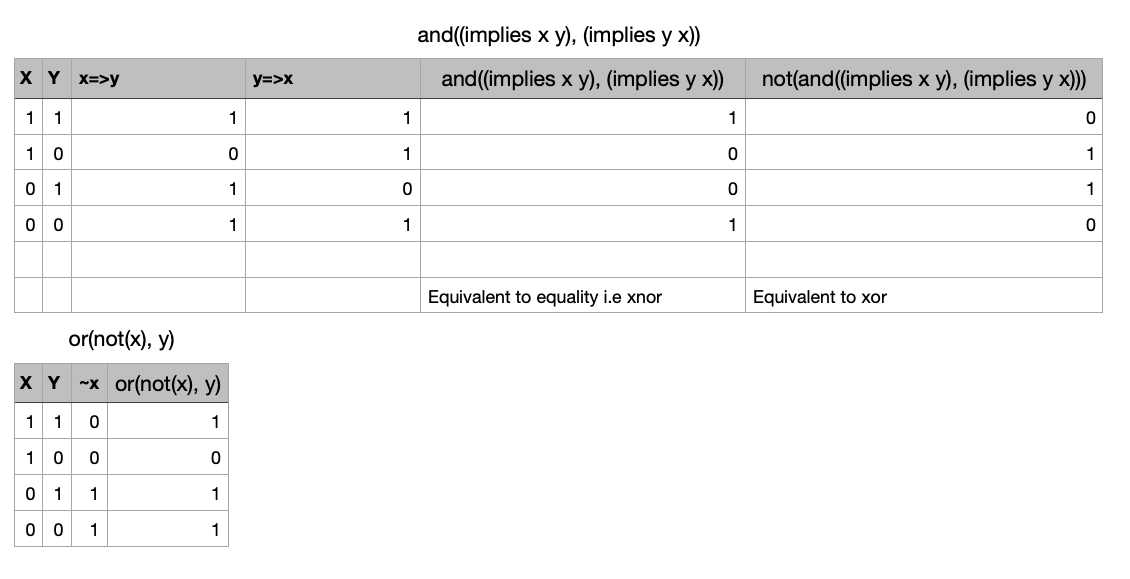
So I remembered noticing that bi-conditional (i.e if and only if) had the same outputs as EQUALITY. And I remember that bi-conditional was two conditionals going both ways ‘anded’ together.

so:

and(x⇒y, y⇒x) = x⇔y = equality

I knew from previously that equality was equivalent to xnor so:

not(equality) = xor

so if I can express IMPLIES in AND, NOT, OR, I can express them all. I remembered from my reading trying to understand the conditional operator that the expression P⇒Q was equivalent to ~PvQ so

implies = or(not(x), y)

so all of them expressed in terms of OR, NOT, AND:

nor = not(or)
implies = or(not(x), y)
equality = and(or(not(x), y), or(not(y), x))
xor = not(and(or(not(x), y), or(not(y), x)))

~30mins

Table working:

---

I don’t think I like, figured figured this out. Think the important/hard bits of this were luckily solved by things I happened to encounter already and couldn’t claim to fully understand. I don’t know if I would’ve figure out the fact that ~p v q is equivalent to p ⇒ q on my own.

[LMD]

Interesting to me is that implies is a more ‘basic’ operation than xor.

[Elliot]

@LMD

xor is true if the inputs are different, and false if they’re the same.

identity is true if the inputs are same, and false if they’re different.

right so not(xor) = identity and not(identity) = xor

identity(x) = x

And identity only takes one input. I think you’re mixing up identity with something else?

[LMD]

Oh sorry, thats a typo. I meant not(xor) = equality and not(equality) = xor.

[Elliot]

@LMD

nor = not(or)
implies = or(not(x), y)
equality = and(or(not(x), y), or(not(y), x))
xor = not(and(or(not(x), y), or(not(y), x)))

Good. Look for other ways to do equality and xor.

[LMD]

I did find another way to do equality and xor. ~ 20mins

XOR = and(or(not(x), not(y)), or(x, y))
Equality = not(and(or(not(x), not(y)), or(x, y)))

[Elliot]

If you work on equality directly instead of inverting xor, you can find a different solution.

[LMD]

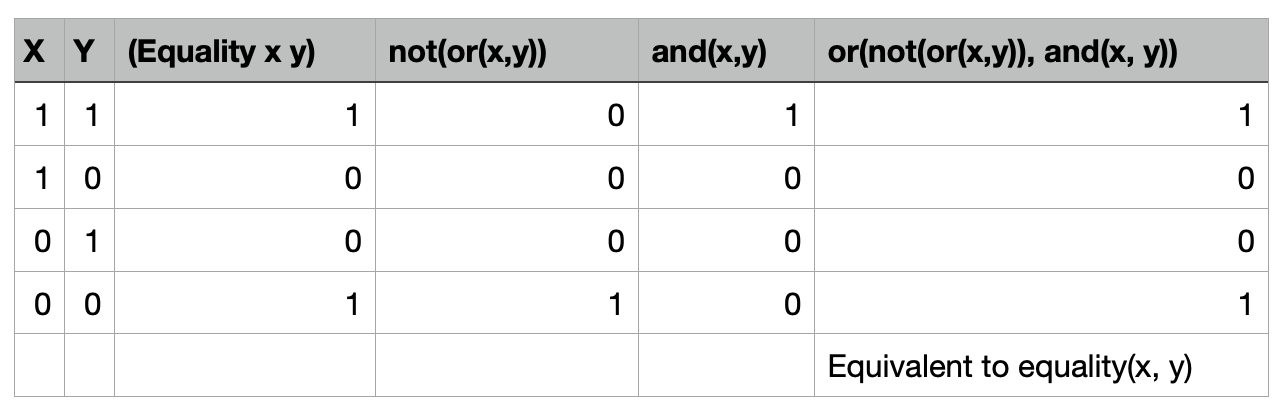
Okay, yup I found another solution for equality:

equality(x, y) = or(not(or(x,y)), and(x, y))

~9mins.

[LMD]

Interesting so AND and OR do opposite things when the inputs are different. But when the inputs are the same, they both do the same thing, that is the behave like an identity gate. So an AND and OR gate both preserve the inputs when they are equal, but one(AND) outputs false when the inputs are different, and OR outputs true when the inputs are different.

So an AND kind of behaves like an Identity gate and a zero gate. And an OR behaves like an identity gate and a one gate. With equal inputs it functions as an identity gate, and with unequal inputs they function as either a zero(AND) or one(OR) gate.

[LMD]

Similarly, here is a solution for XOR that isn’t just a negation of equality:

xor = and(or(x, y), not(and(x, y)))

[LMD]

Next from Eternity’s thread:

@Elliot

Can you come up with a universal set of logic operators that is smaller than {and, or, not}? How can you determine if a set of logic operators is universal (both in general or the easier version: using as a premise that {and, or, not} is universal)?

15-60min

So two or three questions

• 1. Can you come up with a universal set of logic operators that is smaller than {and, or, not}?

• 2a. How can you determine if a set of logic operators is universal in general?

  or, easier:

• 2b. How can you determine if a set of logic operators is universal using a premise that {and, or, not} is universal)?

A universal set of logic operators can be arranged to perform all other logic operations. All logic operations could be expressed in terms of this smaller set of operators. This is what makes the set universal. This is what a universal set of logic operators means.

There can be multiple universal sets. For example, the set of all logic operators is also universal. Just because a set is universal doesn’t mean its members can’t be expressed using less operations.

{and, or, not} is a universal set. But if any one of them could be expressed in terms of the others, you could have a smaller set. If OR can be expressed in terms of just {and, not} then {and, or, not} isn’t as fundamental a set as {and, not}. This reminds me of the assignment to try to figure out De Morgan’s laws for converting AND and OR into each other.

If I can find a way to convert one to the other then I can have a smaller universal set. And if neither of those two remaining operators can be reduced to the other, and I know that {and, or, not} is universal, then I know that any set that includes both of them is universal.

2b. How can you determine if a set of logic operators is universal using a premise that {and, or, not} is universal)?

My answer to 2b: If the set contains {and, or, not} or the set of operations that {and, or, not} can be expressed in.

1. Can you come up with a universal set of logic operators that is smaller than {and, or, not}?

If it’s possible to represent OR using only AND and NOT, or AND using only OR and NOT, then it’s possible. I’ll give it a go again.

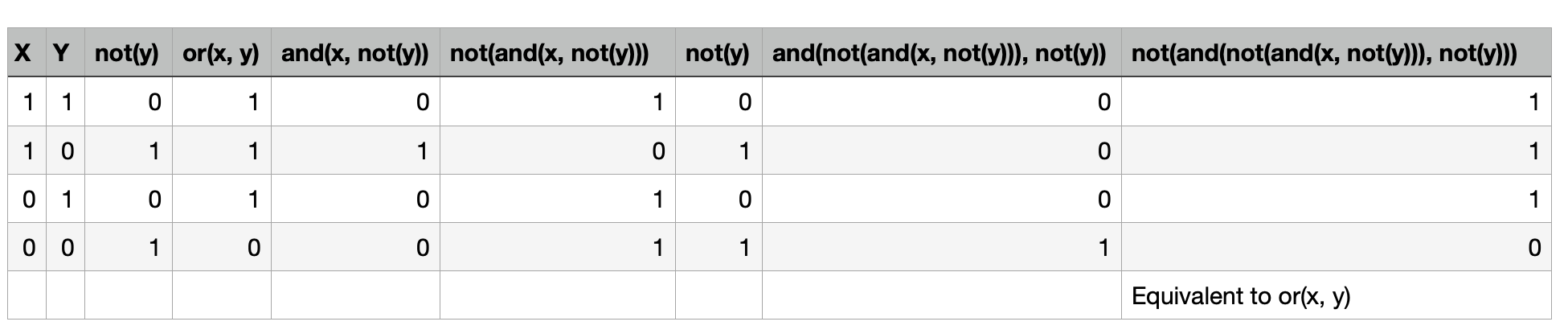
@45mins. Okay I believe I found a solution. I can express or(x, y) only in terms of {not, and}:

or(x, y) = not(and(not(and(x, not(y))), not(y)))

Truth Table:

So, if i’m not mistaken, my answer to 1. is yes: {not, and} is smaller than {or, and, not} and if {or, and, not} is universal then {not, and} is too.

2a. How can you determine if a set of logic operators is universal in general?

I’m running out of time. You could just see if you can express all logic operators in them. But I think you would need an explanation of why you could express all logic operator in terms of {and, not, or}. I don’t know an explanation.

~56mins.

[LMD]

@LMD

You could just see if you can express all logic operators in them. But I think you would need an explanation of why you could express all logic operator in terms of {and, not, or}.

Also, you might not find ways to express them by just trying. But from this alone you wouldn’t be able to decide it wasn’t possible. You’d need an explanation of why you couldn’t do it.

[Elliot]

@LMD

or(x, y) = not(and(not(and(x, not(y))), not(y)))

Check this expression directly with all 4 input cases (11 10 01 00).

[Elliot]

@LMD

My answer to 2b: If the set contains {and, or, not} or the set of operations that {and, or, not} can be expressed in.

yes

@LMD

If OR can be expressed in terms of just {and, not} then {and, or, not} isn’t as fundamental a set as {and, not}.

I wouldn’t necessarily equate a smaller set with being more fundamental.