This is like talking to Rami… You’d ask Rami what he meant and he’d look up words from his own sentence in the dictionary to try to figure out what they mean. It’s like he can’t remember, or never knew, what he meant.
EDIT: Oops I didn’t notice the category. I think it’s a serious problem that will prevent doing well at the project, but never mind.
Good point.
No I did not. I’ll try that now.
The problem tells us three things:
I. The three lines intersecting at O - \overline {BE}, \overline {CF} & \overline {AD} - are straight lines
II. ∠COD = ∠DOE
III. Ratio of ∠COB to ∠BOF is 7:2
Ok I see the issue…
Somehow I skipped over II and didn’t use that.
Based on the information in the problem, we can deduce that ∠COB = 140° and ∠BOF = 40°. ∠BOF is a vertical angle to ∠COE, so ∠COE is also 40°. ∠COE is composed of two angles, ∠COD and ∠DOE, which are equal to each other, and so the 40° of ∠COE must be equally divided amongst these two angles. So I think that ∠COD = 20°.
As a methodology improvement, I think I should try writing out the information that is given by the problem, without doing any deductions from that information, in a separate section of my answers, so that I make sure I’ve got it straight what information I have and what information I’m adding.
Another problem I found tricky. Comments/crits about how I approached the problem, good ways to think about it, and so on, are welcome. I talk about their solution a bit at the end.
IF a transversal cuts two lines such that the same-side interior angles sum to 180°,
THEN the two lines are parallel.
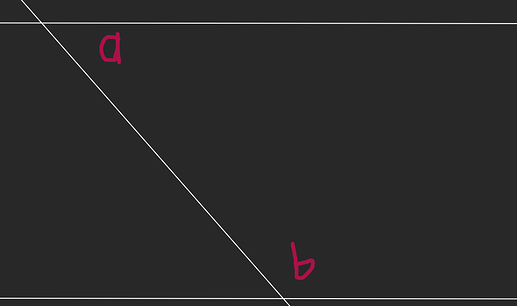
Suppose a and b are the same-side interior angles
Let’s briefly consider what the situation would be like if the lines were parallel. This is not my proof or answer to the question - this is just setting out some relevant background.
The transversal would cut the angles equally on both lines, which means that the corresponding angle for a on the other parallel line, which I’ve labeled a’, will have the same value as a.
Since a’ appears on a line with b, a’ + b (and a + b) must equal 180°. So a and b are supplementary.
Let’s suppose that the transversal cuts the two lines in such a way that the same-side interior angles are supplementary, and see if that can happen with non-parallel lines. In other words, let’s change our diagram a bit and suppose that our lines meet.
If the lines were not parallel, then could the same-side interior angles ∠A & ∠B be supplementary?
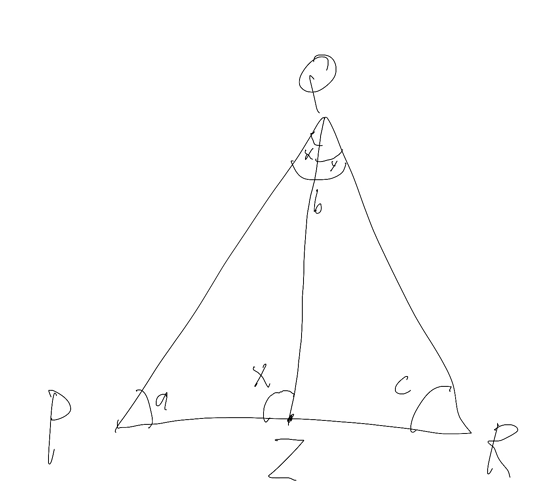
So suppose we reason that a’ + b = 180, and thus a + b must equal 180°. But if we follow that reasoning, we have an issue - a + b appear inside a triangle in our new diagram, and if they sum to 180°, that leaves no angle left over for the remaining angle! So if a transversal cuts two lines such that the same-side interior angles are supplementary, it cannot do so for non-parallel lines (for lines that ever meet) - the lines must be parallel!
I wanted to make sure this worked logically:
IF it is not the case that two lines are parallel,
THEN it is not the case that the same side interior angles of the two lines are supplementary.
(A = two lines are parallel, B = same side interior angles of the two lines are supplementary.)
Logical statement of the above with variables:
IF ¬ A,
then ¬ B.
contrapositive:
IF B,
THEN A.
Replacement of the variables in the contrapositive with their referents:
IF same side interior angles of the two lines are supplementary, then the two lines are parallel.
They had a different approach:
Their approach:
Cuz ∠HBF and ∠FBA are on a straight angle,
I. ∠HBF + ∠FBA = 180°.
Assume:
II. ∠FBA + ∠BAD = 180°.
II can also be represented as ∠HBF = 180° - ∠FBA.
So ∠HBF = 180° - ∠FBA = ∠BAD
When they say that they showed in the text that ∠HBF = ∠BAD implies that \overleftrightarrow {CD} || \overleftrightarrow {EF} , I think they’re referring to their solution to Problem 2.24, where they did a proof by contradiction. They just refer to it here, but I basically did a variation of it in the course of my own answer. So I think our answers are compatible in that regard.
I realized I made a mistake in my answer on the final problem. 2.57, before checking the answer in the book, and I’ve been a bit stuck on it. I will write something tomorrow. Have gone through all the problems other than that
I was distracted by an issue I was having in another topic and didn’t follow up on this as soon as I intended. Going to follow up now. I’ve been stuck on this problem for a while. Thoughts welcome. Work so far shown below.
Information in the problem:
∠PQR - ∠PRQ = 42°
Point Z lies on \overline{PR} of △PQR such that:
∠PZQ = ∠PQZ
Depiction (not to scale) of triangle based on given information:
Equations for the three triangles in the problem:
△PQR = ∠PQR + ∠QRP + ∠RPQ = 180°
△PQZ = ∠PQZ + ∠QZP + ∠ZPQ = 180°
△QRZ = ∠RQZ + ∠QZR + ∠ZRQ = 180°
Manipulation of expression for △PQR
∠RPQ = 180 - (∠PQR + ∠QRP)
Expression in the hint:
∠RQZ + ∠ZQP = ∠RQP
Expression showing subtraction of ∠RQZ from ∠PQR to make ∠PQZ
∠PQR - ∠RQZ = ∠PQZ
Transformation of previous expression:
∠PQR = ∠PQZ + ∠RQZ
Since Z appears on line \overline{PR}, the exterior angle for ∠QZR is the angle ∠PZQ. The exterior angle is the sum of the remote interior angles. So exterior angle for ∠QZR = ∠PZQ = ∠ZQR + ∠QRZ. Note also that we were told ∠PZQ = ∠PQZ. So
∠QZR = ∠PZQ = ∠PQZ = ∠ZQR + ∠QRZ.
For an equation involving ∠PRQ and ∠ZQR:
The ∠R angle is shared between the triangles △PQR and △QRZ. In other words, ∠ZRQ = ∠PRQ.
Let’s start with a triangle equation:
△QRZ = ∠ZQR + ∠QZR + ∠ZRQ = 180°
Now let’s substitute ∠PRQ for ∠ZRQ
∠ZQR + ∠QZR + ∠PRQ = 180°
So we have ∠ZQR and ∠PRQ, but we also have ∠QZR. can we get rid of it?
For an equation involving ∠PZQ and ∠ZQR:
∠ZQR + ∠QRZ = ∠PZQ
I. ∠ZQR + ∠QZR + ∠PRQ = 180°
II. ∠ZQR + ∠QRZ = ∠PZQ
Add I and II together:
2∠ZQR + ∠QZR + ∠QRZ + ∠PRQ = 180° + ∠PZQ
∠PQR = ∠PQZ + ∠RQZ
∠PZQ = ∠PQZ
I succeeded according to my stated goal of at least attempting “all the exercises in the chapter in some reasonable amount of time.” I had at least attempted all the exercises before temporarily leaving the forum.
I wound up looking at the answer on the very last problem (Exercise 2.57), but still don’t fully understand it. I intend to double back to that at some point.
I spent a lot of time lingering on 2.57 unproductively. I think that was a mistake.
I think I learned a bit more about geometry. I also had some connections between my problems solving geometry problems and my problems thinking about philosophy pointed out by others, so that seemed like a benefit.
Your post is pretty unreadable. Can you solve it if you make it more organized and readable? Like using one letter variables that make sense, and putting stuff in the diagram. Like this:
Thanks for the suggestion. I think it helped but I’ve still been having trouble solving the problem. Below is as far as I have gotten that I am confident about (I’ve been trying different things but going in circles a bit as before, so I figured I’d shared the stuff that seemed solid).
Following what you suggested: let’s call angle at point P = ∠a.
Angle at point R = ∠c.
∠PQZ = ∠x. Since ∠PZQ = ∠PQZ, ∠PZQ will also be ∠x.
∠RQZ = ∠y.
Let’s call the sum of ∠x and ∠y (in other words, the entire angle at point Q) ∠b.
Depiction (relationships not to scale):
Also, note that based on the information we were given, ∠b - ∠c = 42°.
Equations for the three triangles in the problem:
△PQR = ∠a + ∠b + ∠c = 180°
△PQZ = ∠x + ∠x + ∠a = 180°
or
2∠x + ∠a = 180°
△QRZ = ∠y + (180 - ∠x) + ∠c = 180°
or
y + (180 - (∠y + ∠c)) + ∠c = 180°
or
(∠y + ∠c) - ∠x = 0
or
∠x = ∠y + ∠c
(this makes sense since ∠x is the exterior angle of ∠QZR and has to be equal to the sum of the remote exterior angles ∠y and ∠c.)
Is there a reason you ignored this part of the suggestion:
I did not think I had ignored it 
None of your variables are actually single letter variables.
E.g.:
As single letter variables, that would be:
x = y + c
You also used 4-character variables and degrees in your equations, e.g.:
I actually can’t tell here if the “or” means you are giving a different, independently arrived at equation from the one above, or if you are using “or” when you simplify the equation above. Some of them look like simplifications, but some do not.
oic. I wasn’t counting the ∠ symbol as a letter. I can redo what I wrote with that changed.
I’m not trying to be argumentative below. I am just trying to say what I am thinking. I might be totally wrong.
I interpreted Elliot’s suggestion as being about indicating the angles with one-letter variables. I see the point of Elliot’s suggestion when interpreted in that way, because I think indicating the angles with one-letter variables helps readability a lot. We need to show various relationships between the angles and having single-letter expressions helps do that concisely.
I don’t see the benefit of representing the triangles with one letter variables. I could initially declare that △PQR = J or something, but I’m not sure what the benefit would be. I would also have to keep that mapping in mind, which seems like a downside.
I didn’t consider applying the idea of using one letter variables to actual numbers like 180°. I don’t see the point of replacing 180° with a variable. If it was a really big number, I could see the point, but it’s a small, standard value, so it seems fine to leave it.
Yeah I used “or” super unclearly. I’ll try indicating what I’m doing much more unambiguously when I rewrite things.
BTW I looked up the geometry book on the AOPS website and it said, in the context of describing a class that covers the book:
This is the most challenging of our Introduction series of classes. We recommend that students complete our Introduction to Algebra B course, or are able to pass the Introduction to Algebra B post-test, prior to taking Introduction to Geometry.
That got me wondering if I was struggling with some problems cuz of lacking those prerequisites.
I wasn’t counting it as a letter either.
There was some ambiguity in what I wrote. When I said “single letter variables” I meant variables that are only a single letter. So, a single-character variable.
I agree that it helps with readability. It helps in more than one way. I think that what you are thinking of is it makes it easier to see which angle is being referred to each time, and helps to differentiate the different angles from each other more in the equation.
Removing angle signs and units helps with readability in another way too. It makes the equations look more like standard algebra equations. Most people find it easier to do algebra manipulations on simpler looking equations. It is actually a standard recommendation to simplify complex-looking equations, in order to make it easier to do algebra manipulations.
That’s not what I meant. They don’t need to be in the equations at all.
If I was trying to go over this problem with a student, I wouldn’t write the equations the way you did. In my experience, that would just confuse most students.
E.g., I would just write this:
as:
x + x + a = 180
and then simplify to:
2x + a = 180
I would label the equation with what triangle it was (and I might use labels like “left”, “right”, and “whole” for the triangles, instead of the 3-letter triangle names, especially if the student was having any trouble). But I generally do not write out equations with 2 equal signs in them when working with students (unless the problem requires it) because most people find those confusing. (People have enough trouble just understanding what one equals sign means.)
Ah.
yes.
That makes sense.
Ah.
No ° symbol either?
I noticed when I was doing my first attempt at a more readable rewrite that I made an error involving an equal sign in an earlier post.
here’s another attempt at setting up the problem.
EDIT: I’m only trying the initial setup instead of solving it since I think it makes sense to try to get that right before moving onto a solution.
Information in the problem (without any alterations or translations):
∠PQR - ∠R = 42°
Point Z lies on \overline{PR} of △PQR such that:
∠PZQ = ∠PQZ
I’ll use the following variables for the indicated angles:
Angle at point P: a.
Angle at point R: c.
Angle ∠PQZ: x.
Since ∠PZQ = ∠PQZ, ∠PZQ will also be x.
Angle ∠RQZ will be y.
The sum of x and y (in other words, the entire angle at point Q) will be b.
Depiction of above (relationships not to scale):
Also, note that based on the information we were given, b - c = 42°.
Equations for the three triangles in the problem:
Whole Triangle (△PQR):
a + b + c = 180°
Left triangle (△PZQ):
x + x + a = 180°
This can be simplified as:
2x + a = 180°
Right triangle (△QRZ)
Analysis: There are two angles at point Z within our triangle. One of them has the value x and is an angle within the Left triangle. That same angle x serves as an exterior angle for the angle at point Z within the right triangle. An exterior angle and an interior angle must sum to 180°. Therefore, the value of the angle at point Z within the right triangle can be represented as 180° minus x.
y + (180 - x) + c = 180°
This is how I wrote out the information in this post, to make it easier to read for myself (this is without adding any of my own work):
I’m not sure what your background is, and I also haven’t looked at the books enough to know what order I would recommend them.
I have looked at them enough to know that there is no order that I would recommend a student just go through all the books separately, one at a time, in order, without using any other resources. (There are NO math curriculums at all that I would ever recommend that for, for anyone.)
Re this particular problem: have you done systems of equations before? That is a prerequisite here.
Was okay at math in grade school. Didn’t do high school math. Did some remedial stuff in college (“College Algebra”, and then a “Pre-Calculus” class that covered a bunch of high school stuff like Trig, and then a Calc 1 class). Forgot a lot of this stuff now.
Yes though I could probably benefit from some review.
