Project Summary
Summary: Do the second chapter of the Art of Problem Solving’s Introduction to Geometry book.
Goal
Goal: Success would be if I at least attempted all the exercises in the chapter in some reasonable amount of time. Failure would be if I dropped the project for a long time.
Metrics: Making regular progress every week. Target rate will be a couple of subchapters per week, and I hope to go faster than that. I’ll slow down if I need to in order to understand some concept and won’t consider needing to slow down for that reason a failure.
Broader goal: Working through whole book and trying to use CF project planning templates more.
Values: I’m interested in learning math. I like math and find it fun.
CF relevance: I think learning math could help with being a more precise thinker, which would be helpful for learning philosophy.
Plan
Plan: Steps are to read the sub chapters in order and then work through the problems. I plan to share some of the work I do for public criticism.
Project size: Small. Only things in scope are the exercises in the chapter.
Resource budget: Some free time.
Asks: If people notice any errors in stuff I write about the project, corrections would be appreciated.
Offers: None.
Independence: I’ll finish the project regardless of whether people say stuff or not.
Confidence: I am very confident the project will be completed. It is small and should be easy and basically review for me.
Follow through: I’d be very surprised if I needed to take a major break. It might take a bit longer than I’d like if I got super busy.
Context
Context: None.
Background: I have some background math knowledge.
Track Record: I’ve had some success doing learning projects before (like with grammar and programming). I did a mini project for the first chapter.
Priorities: I was working on a math book already and got the suggestion that this book might be good to try.
Progress: Looked at book a bit to get an idea of the size of the chapter.
Problems: None.
I’ve gone through 4 subchapters so far, though only two of those were really “meaty” subchapters. Still, progress seems okay.
I completed subchapter 2.5. I made an error in one of the exercises. I misread what the question was asking for and responded with an answer for a different angle than the one they asked.
I actually had the correct information in a diagram that I made - I just like misread the question or something.
WHOOPS! I fell right into the bogus solution 
I know this logic stuff too, such that I can apply it to other contexts, but did not apply it here!
Hmm I’m a bit confused now.
Section 2.4 had this stuff:
That’s the stuff I was trying to use, and which I thought they criticized as bogus answer.
And then for the next problem they say:
\angle DAC and \angle ACB are like, alternate interior angles, aren’t they? So they’re using that relationship again. So I’m confused what their point was re: the “bogus” answer.
The thing they criticized was this:
The thing that was wrong there wasn’t the conclusion – the lines are in fact parallel. The problem is the reasoning they use to get to the conclusion.
(I could explain more, but want to leave it for you to think about more on your own. I can respond more if you have questions or say more though.)
Ok let’s see if I can make some correct statements here. So earlier they said:
So the transversal cutting parallel lines at equal angles is something we verified with some measurements, but in general it’s something we assume, not prove.
So a statement of this Transversal Cutting Parallel Lines at Equal Angles Postulate (Transversal Postulate) might be:
If you have
- a transversal
- cutting parallel lines,
then the lines are going to be cut at equal angles.
With the bogus solution, we started from having equal angles, and went from that to assuming we had parallel lines. They say:
So a statement of the Bogus Solution postulate might be:
In light of the Transversal Postulate, if you have
- a transversal cutting lines at equal angles
then the lines are parallel.
The Bogus Solution postulate is something we could assume on its own (as like a new assumption separate from the Transversal Postulate), or it is something we could prove, but it’s invalid to reason from the Transversal Postulate in the way we did.
Having trouble with this problem
Just flagging it for now. Will try to say more later.
(I have not compared this analysis to the book’s yet)
Regarding the first sentence in problem 2.7.2, I think they’re referring to the proof by contradiction in problem 2.24. Cuz they’re saying they proved that if you have particular angles that are equal, then that shows that lines are parallel (rather than starting from the lines being parallel and then reasoning that the angles must be equal).
So here is my statement of the background and problem:
Assume that if n cuts k and m such that x = y, then k is parallel to m.
Assume that y = z
And we want to prove that k is parallel to m
Based on the diagram, x must equal z because they are vertical angles.
And y must equal its vertical angle - let’s call it w.
So y = z
x = z
y = w
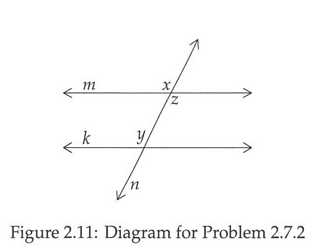
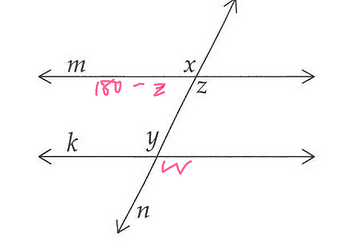
The angle that’s supplementary to both x and z must equal 180 - z and 180 - x.
We were given that z = y. So we can substitute y in in 180 - z
So then we have 180 - y and x as supplementary angles.
You can always define a supplementary angle to another angle in terms of 180 less that angle, since what it means to be supplementary is that two angles add up to 180. Given that fact, 180 - x would be an appropriate expression of the supplementary angle to x. 180 - y is identical in form, except that it uses y, not x. This shows that x and y are equal and, given what we already know, that the lines are parallel.
i think my answer was not wrong but I could have saved a lot of work  :
:
PURE LOGIC QUESTION (I got it right - I just like sharing LOGIC stuff):
wondering if i answered 2.46 in a reasonable way. i have a harder time with this kind of thing. Haven’t checked the book yet.
2.46
Suppose a and b are the same-side interior angles
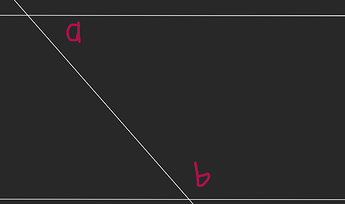
Let’s briefly consider what the situation would be like if the lines were parallel. This is not my proof or answer to the question - this is just setting out some relevant background.
The transversal would cut the angles equally on both lines, which means that the corresponding angle for a, which I’ve labeled a’, will have the same value as a.
Since a’ appears on a line with b, a’ + b (and a + b) must equal 180°. So a and b are supplementary.
Let’s suppose that the transversal cuts the two lines in such a way that the same-side interior angles are supplementary, and see if that can happen with non-parallel lines. In other words, let’s change our diagram a bit and suppose that our lines meet.
(img)
If the lines were not parallel, then could the same-side interior angles ∠A & ∠B be supplementary?
So suppose we reason that a’ + b = 180, and thus a + b must equal 180°. But, uh oh, if we follow that reasoning, we have an issue - a + b appear inside a triangle in our new diagram, and if they sum to 180°, that leaves no angle left over for the remaining angle! So if a transversal cuts two lines such that the same-side interior angles are supplementary, it cannot do so for non-parallel lines - the lines must be parallel!
did an initial pass on all the problems in chapter 2. Some of them seemed challenging but not too hard and I didn’t get too stuck on any. Will check my answers soon.
BTW I think making full, effective use of my actual computers (as opposed to trying to do math on ipad) has been helpful with math stuff. I think maybe I was using inferior methods before to try to somewhat copy how I learned math in school or something … but I didn’t learn it that well, so uhh…
I’m wondering whether assuming I can divide the vertical angle evenly based on the picture is something that is a reasonable assumption. I have trouble figuring that kind of thing out. (I got the right answer, and my answer seems compatible with the way the book did it)

Was reviewing my answer to this problem (haven’t checked book’s answer yet) and decided that my own answer was inadequate. So I’ve actually been a bit stuck on this problem.
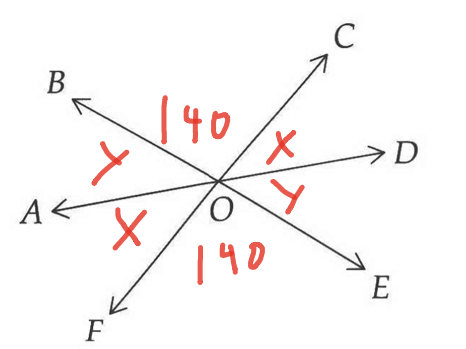
Basically I assumed that \overline {AD} split ∠BOF and ∠COE perfectly in two, but I’m not sure that assumption is actually warranted. So I tried seeing if I could figure out the answer without that assumption, but I haven’t been able to so far. Below is what I’ve figured out. Thoughts/hints welcome. This problem doesn’t have an included hint.
∠COB and ∠BOF have to add up to 180° since they’re on a straight line. With the given ratios, this means that ∠COB is equal to 140° and ∠BOF is equal to 40° (since 7 + 2 = 9, so we divide 180° by 9 and then multiply it by the numbers in the ratio).
We can also surmise that ∠FOE is 140° since it is a vertical angle to ∠COB.
Here are some other relationships we can determine:
I. ∠BOF = ∠COE = 40°
II. ∠AOF = ∠COD
III. ∠BOA = ∠DOE
IV. ∠AOF + ∠BOA = ∠BOF
V. ∠COD + ∠DOE = ∠COE
Let’s call the measure of II x and the measure of III y.
So x + y = 40°
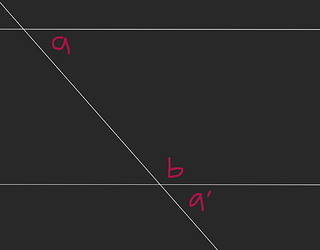
I tried thinking about it another way:
Let’s add a line to the diagram that splits the 140° angles into two 70° angles.

We knew that 140° + x + y = 180°.
With the new diagram, it would appear that 70° + x = 70 + y = 90°, since we evenly divided a 140° angle and since the sum of half that 140° angle + x or y appears to be a right angle.
I haven’t looked at the whole problem yet, so not replying to the whole thing, just this part.
Are you saying that you are assuming that the angle is a right angle because it looks like a right angle in the picture?
Yeah.
I was trying not to do that but that is where I landed based on what I wrote…
I had some other relevant thought though, so let me try to describe that. The thought is something like, we have 140° + x + y = 180° cuz they’re all on a straight line. Cut the 140° in half, so that it’s 70°. And then I think I made some kind of error in reasoning or had fuzzy thinking or something and assumed that because we split the 140° into two parts, each part + the x or y that was next to it should add up to 90°, since the whole thing adds up to 180°. Something like that.
Doesn’t make sense. One thing is that you could have x = 10° and y = 30° and 140° + x + y = 180°. So I need some idea that addresses that issue instead of just assuming that possibility away.
I just looked at the initial question. Given that it says that the ratio of COB to BOF is 7:2, while those two angles actually look close to equal to each other, I think it’s pretty unreasonable to base any assumptions on what the angles look like.
When you read the initial question, did you actually write down all the information from it? I see that you wrote out some of the relationships you think you can determine from the problem, but I don’t see anywhere that actually contains all the information given in the problem.







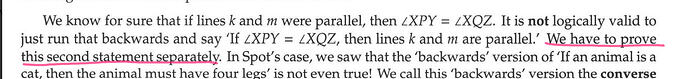

 :
: