It varies some but you can use | (pipe) = or. And ^ = xor
ok what about an expression for:
(x&y) | (!x & y) | (!x & !y)
11 = (1 & 1) | (0 & 1) | (0 & 0) = 1 | 0 | 0 = 1
10 = (1 & 0) | (0 & 0) | (0 & 1) = 0 | 0 | 0 = 0
01 = (0 & 1) | (1 & 1) | (1 & 0) = 0 | 1 | 0 = 1
00 = (0 & 0) | (1 & 0) | (1 & 1) = 0 |0 | 1= 1
Use “or” to combine the different “and” expressions that give you true for only a single set of inputs.
So if you wanted a truth table where it goes:
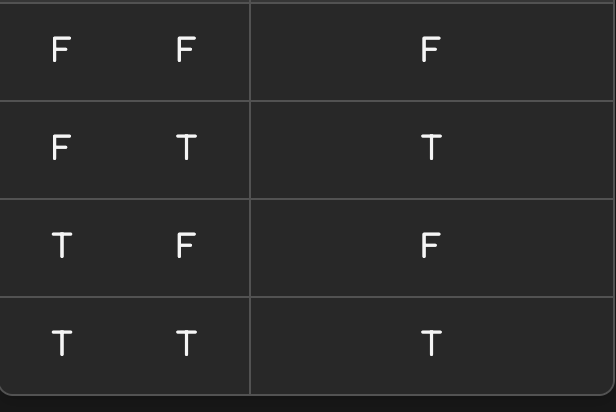
You would just “or” the two “and” expressions that give you true for those lines. In this case:
(~x & y) | (x & y)
I think you were close to this before but you were trying to do something with the false rows too. Does stuff make sense now?
Yes. I looked over my previous answer and yeah looks like I was close.
So can you write English instructions that someone else could follow to make an expression with {and, or, not} for any truth table?
Like a set of step-by-step instructions?
1.) Pick a truth table you want to create. We’ll use the conditional as an example:
2.) For each true line of the truth table come up with an expression using {and. not} that outputs true for the inputs for that line. For example, (!x & !y), (!x & y), (x&y).
3.) Combine the individual expressions from step 2 into one whole expression using {or}. For example, (!x & !y) | (!x & y) | (x&y).
What do you do with false rows or why do you do nothing?
You can ignore false rows. This is because expressions with “and” are true for only two (or, whatever number, all) inputs. For example, (x & !y) is true when x is true and when y is false. It is false, for every other set of inputs. If you combine multiple of these and statements using “or”: (x & !y) | (!x & !y). It creates true outputs for each of those expressions, since its “x and not y” or “not x and not y”. The rest stay false and it doesn’t create an issue.
Uhh. I thought about that for a brief moment. My quick response is to create a truth table with all true outputs and then “not” the whole expression. So: !((x & y) | (~x & y) | (x & !y) | (!x & !y) ).
Is there a simpler way to do it?
What if one row needs to be false. Is there something you can optionally add to the expression to handle that case? If you were to add something, what should its value be for the inputs for that row? And what should its value be for other inputs?
Uhhh. Just write true expressions for all true rows and leave the false row alone.
!((x & y) | (~x & y) | (x & !y) | (!x & !y))
This expression? I don’t think so. If you remove the “!” that not’s the whole expression and get:
(x & y) | (~x & y) | (x & !y) | (!x & !y). You have all true’s and you can not any one of the and expressions to get false for that line.
Ok I think I’m confused as to what you’re asking. Maybe a re-word would help?
The expression for a truth table of all false is: F
The expression you can add to handle false rows is F, which gives the desired output for the target row and false for all other rows, just like the expressions you construct for true rows.
Having “or F” one or more times is unnecessary but harmless and makes it easier to see how a truth table with all F outputs works: you get: F or F or F or F which you can simplify to just F. (F or F = F)
make sense?
Expression like: (!x & y). Like the unary expressions from the beginning? Meaning the truth table would be:
11 = F
10 = F
01 = F
00 = F
because it’s always false. Right?
So (x&y) | F. Ok that makes sense. It’s (x&y) or it’s false.
I think so? Is my working/understanding ok?
OK, so do you see how “F” is a simpler way to do it?
Yes.
I was still caught up on coming up with a way to answer :
In terms of {and, or, not}. It makes sense though to just use F.
OK, so suppose T and F (and 1 and 0) aren’t in your toolkit. You can only use: {and, or, not} and variables. How can you construct T or F? Your answer must work for all possible values the variables could have.
All possible values for the variables are:
TT
TF
FT
FF
So would this be fine for always true: (x & y) | (~x & y) | (x & !y) | (!x & !y). No matter what two inputs are put in it will always be true.
For false it would be !((x & y) | (~x & y) | (x & !y) | (!x & !y)).
So if I did have T and F in my toolkit. Before it was something like (x&y) | F. Now it’s (x&y) | !((x & y) | (~x & y) | (x & !y) | (!x & !y)). It works out the same.
Is this fine? Or?