Next from Eternity’s thread:
So two or three questions
-
- Can you come up with a universal set of logic operators that is smaller than {and, or, not}?
-
2a. How can you determine if a set of logic operators is universal in general?
or, easier:
-
2b. How can you determine if a set of logic operators is universal using a premise that {and, or, not} is universal)?
A universal set of logic operators can be arranged to perform all other logic operations. All logic operations could be expressed in terms of this smaller set of operators. This is what makes the set universal. This is what a universal set of logic operators means.
There can be multiple universal sets. For example, the set of all logic operators is also universal. Just because a set is universal doesn’t mean its members can’t be expressed using less operations.
{and, or, not} is a universal set. But if any one of them could be expressed in terms of the others, you could have a smaller set. If OR can be expressed in terms of just {and, not} then {and, or, not} isn’t as fundamental a set as {and, not}. This reminds me of the assignment to try to figure out De Morgan’s laws for converting AND and OR into each other.
If I can find a way to convert one to the other then I can have a smaller universal set. And if neither of those two remaining operators can be reduced to the other, and I know that {and, or, not} is universal, then I know that any set that includes both of them is universal.
2b. How can you determine if a set of logic operators is universal using a premise that {and, or, not} is universal)?
My answer to 2b: If the set contains {and, or, not} or the set of operations that {and, or, not} can be expressed in.
1. Can you come up with a universal set of logic operators that is smaller than {and, or, not}?
If it’s possible to represent OR using only AND and NOT, or AND using only OR and NOT, then it’s possible. I’ll give it a go again.
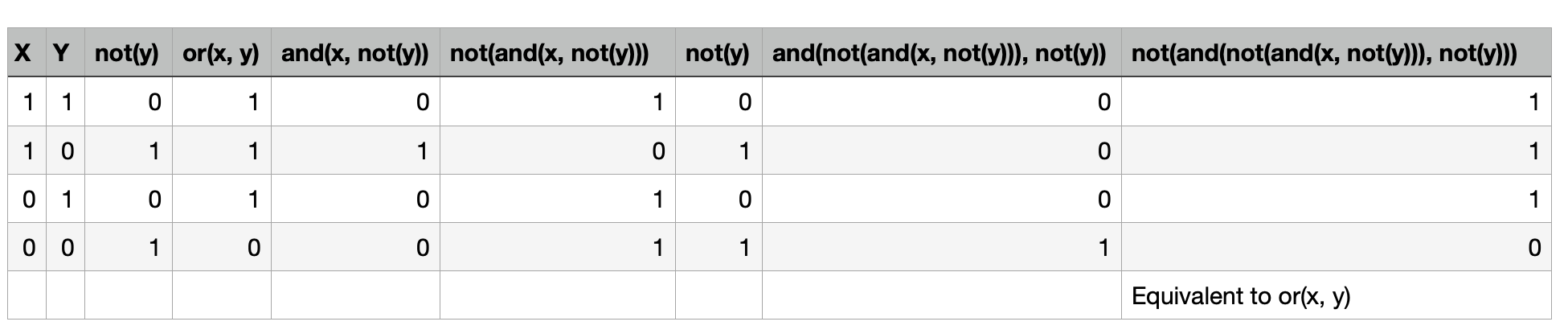
@45mins. Okay I believe I found a solution. I can express or(x, y) only in terms of {not, and}:
or(x, y) = not(and(not(and(x, not(y))), not(y)))
Truth Table:
So, if i’m not mistaken, my answer to 1. is yes: {not, and} is smaller than {or, and, not} and if {or, and, not} is universal then {not, and} is too.
2a. How can you determine if a set of logic operators is universal in general?
I’m running out of time. You could just see if you can express all logic operators in them. But I think you would need an explanation of why you could express all logic operator in terms of {and, not, or}. I don’t know an explanation.
~56mins.