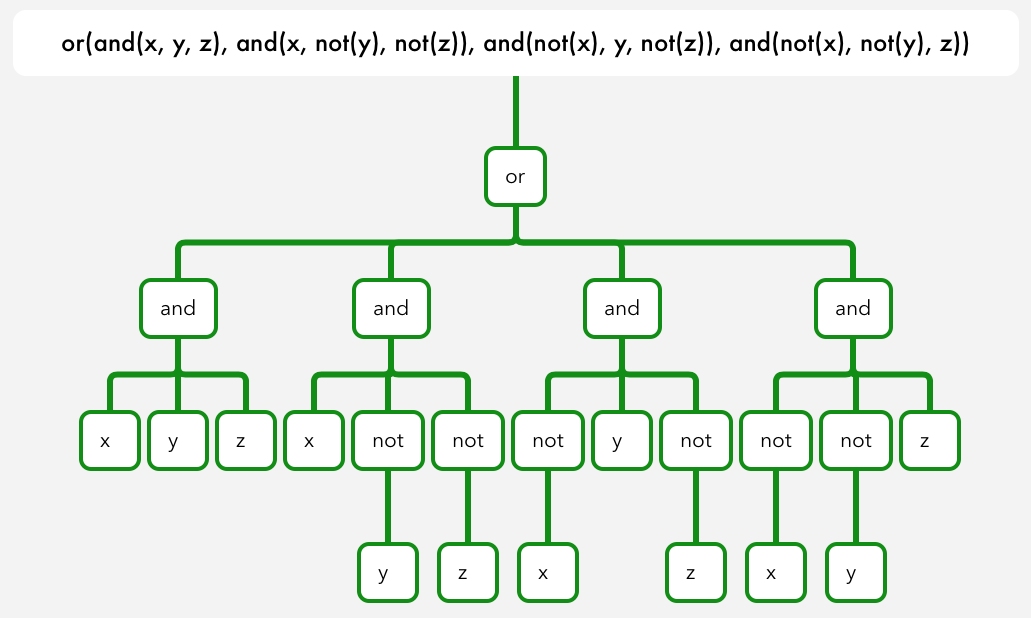
Okay, the 3 input XOR infix expression I did here is:
(x^y^z)v(x^~y^~z)v(~x^y^~z)v(~x^~y^z)
this in prefix:
or(and(x, y, z), and(x, not(y), not(z)), and(not(x), y, not(z)), and(not(x), not(y), z))
the tree of this:
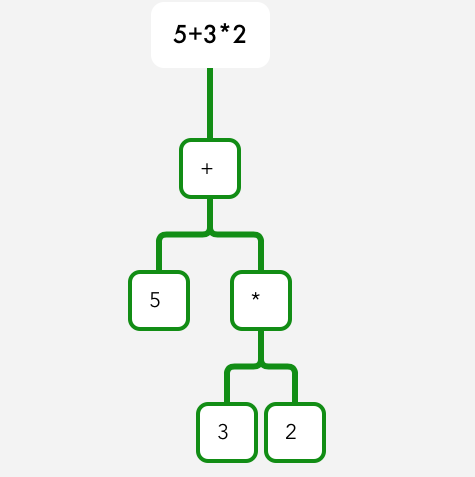
5 + 3 * 2:
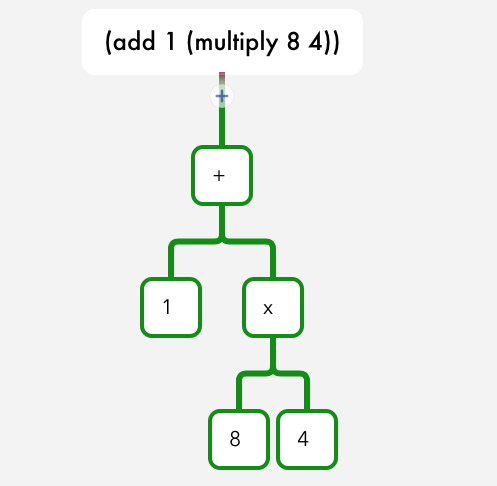
(add 1 (multiply 8 4)):
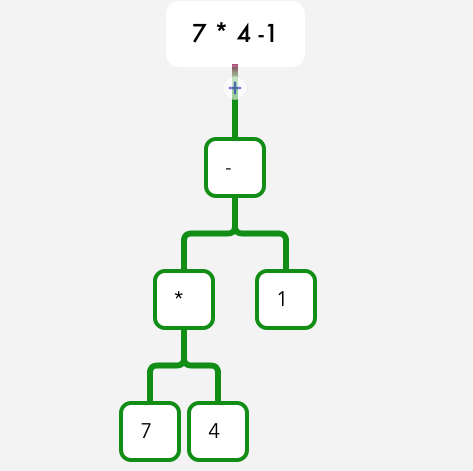
7 * 4 - 1:
(multiply 6 (minus 5 3))
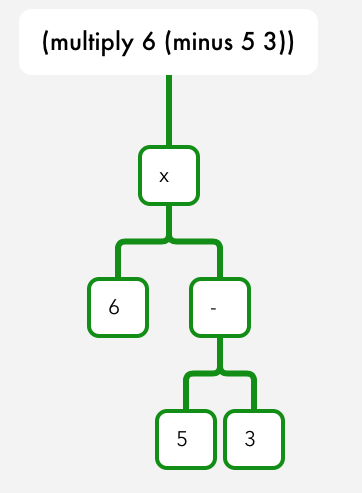
Yes I can really see how much easier it is translating a prefix expression to a tree. With infix you have to read through the whole expression, consider the order of operations, and consider how to diagram it. With prefix you can just go left to right and you start with the highest level. Then you can drop down and back up as you go.