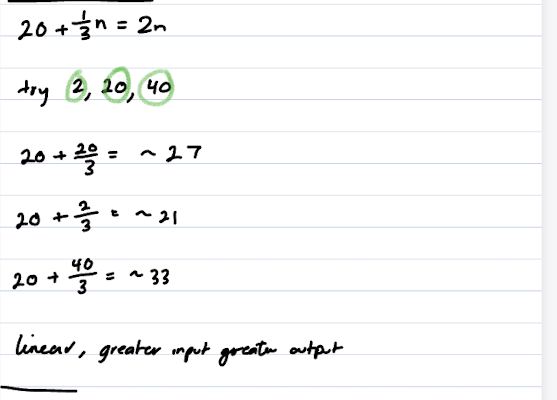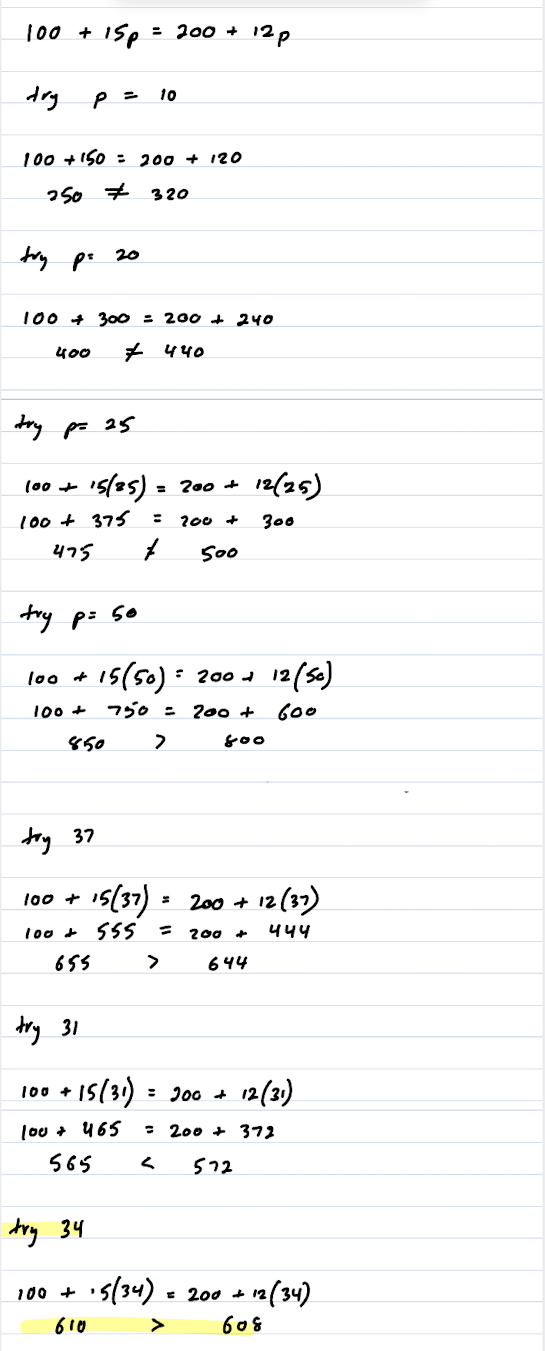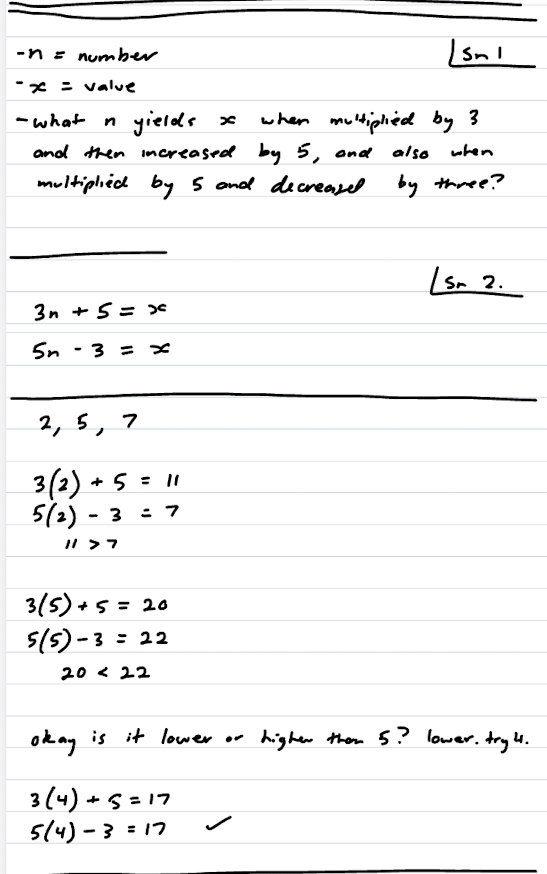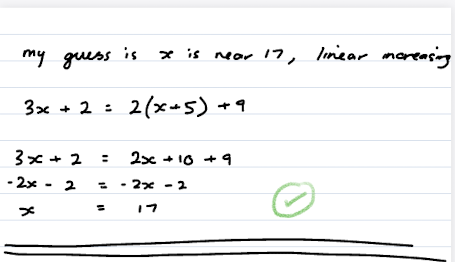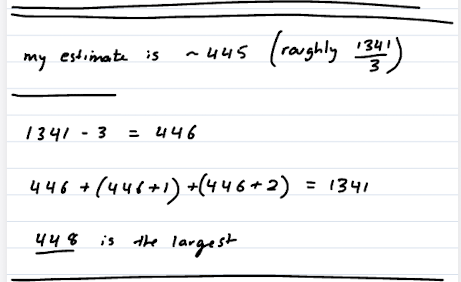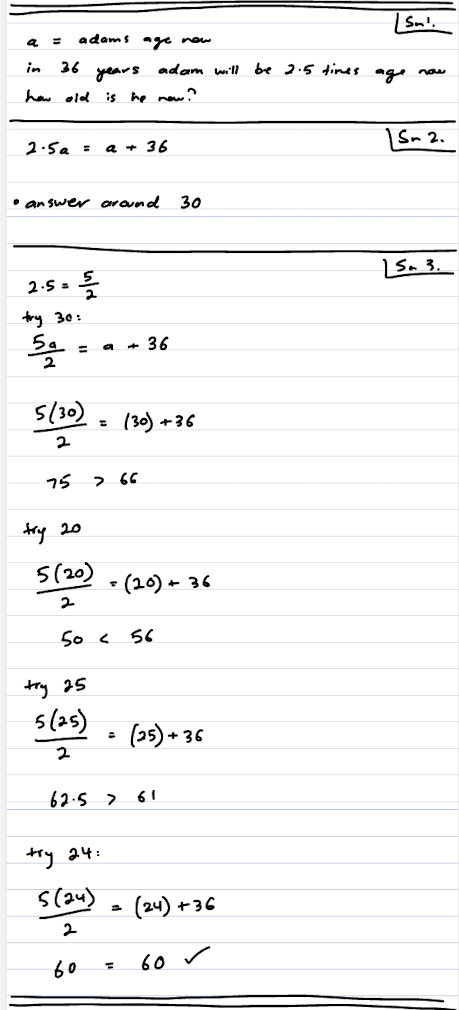LMD Async Tutoring

[LMD]

Here are 5 problems from Alcumus on ‘normal’ difficulty. All the answers were correct. I timed the last 3.

---

1. Joe multiplies a number by 4, adds 1, and then divides by 3, getting a result of 7. Sue divides the same original number by 3, adds 1, and multiplies by 4. What result does she get? Express your answer as a common fraction.

---

2. The \$4.55 in Carol’s piggy bank consists of quarters and nickels. There are seven more nickels than quarters. How many nickels does Carol have in her bank?

---

3. Six friends went to a restaurant and agreed to share the bill equally. However, two people forgot their wallets so the other four friends’ portions of the bill went up by \$7 each. How many dollars was the total bill?

---

4. The bottom cup in a 73 cm tall stack of nested identical cups is 10 cm tall. If each additional cup adds 1.5 cm to the height of the stack, how many total cups are in the stack?

---

5. One caterer charges a basic fee of \$100 plus \$15 per person. A second caterer charges a basic fee of \$200 plus \$12 per person. What is the least number of people for which the second caterer is cheaper?

---

[Elliot]

@LMD

@Elliot

Like if you read the problem, do you intuitively know if the solution should be more or less than 20?

My intuition would say that the ‘result’ (double the number) was over 20, but not necessarily that the number (n) was more or less than 20.

OK so intuition for numbers can be improved with practice. Here is a way to practice it for this problem and many others. This is often best to do before you start solving the problem, but can be done later too.

Take the problem and try a low, medium and high number. (For multi-variable problems, you can do low,low, low,medium, etc. and get 9 pairs, or can do 4 pairs with only low and high, or can keep one unchanging while changing the other variable. There are more options.)

So in this case, for medium I’d pick 20. For low, I’d pick 2, but 10 would be fine as well. The reason for 2 is that negative numbers, 0 and 1 can all be special cases, so I just picked the lowest integer that avoids all that. For high, 30, 40 or 100 would all be reasonable choices (representing: add 10, double the 20, or use a number that’s significantly higher). It can be good to have the numbers evenly spaced (e.g. use 10/20/30) but isn’t needed. You can try additional numbers if you think they’ll provide any useful information.

Trying out some numbers in problems can help you get a feel for what the answer may be like (high, low, medium, and other things like negative or positive, or between two numbers).

You can find patterns like as you increase the inputs, the outputs increase. Combine that with knowing that an input of 20 gives a result that’s too low, and you know the solution must be more than 20.

You can quickly narrow the solution down, like if you also try 100 and the output is too big, then the solution is between 20 and 100. Then you can try the midpoint of the range, 60, and narrow it down to a range of 40. For problems with integer solutions, you can actually get the exact answer just by checking the midpoint of the range repeatedly without it taking a ton of steps. Like narrowing down from 80 possible solutions to 1 is doable within 7 steps.

The main point here is to explore the problem by finding out basic information like whether higher inputs cause lower or higher outputs, and whether the change is linear or exponential, and narrowing things down like the answer needs to be big, small or negative. If you do this, it may help you solve the problems, and it’ll definitely help you intuitively understand what’s going on more and give you an extra way to check for errors (know if your answer is reasonable or not).

So try this on the coins problem and some others.

[LMD]

Cool. Here is some working for the previous coins problem, some more previous problems, and with some new word problems where I do this in section 3 instead of solving.

Coins:

more exploring:

This one I couldn’t remember the original answer so was legitimately estimating. It took 7 steps before it was right:

Some before I had solved the problem:

• What is the number that yields the same value when it is multiplied by three and then increased by five as when it is multiplied by five then decreased by three?

• Joe and Mary each pay the same price for a T-shirt. Before they buy it, Mary has \$ 2 more than Joe. To buy the T-shirt, Joe spends \$1 less than \frac{2}{5} of his money, and Mary spends \frac{1}{3} of her money. What was the total amount of money Joe and Mary originally had altogether?

[LMD]

As part of my assignment to write more and post about it occasionally, here is something I wrote today after reading your recent microblogging post.

I find this is also true in my experience writing and playing music with people.

I’ve basically had no luck creating the basic musical ideas of a piece in a group setting. Very little to no progress was made in the projects I was involved in as a writer in this way. It always ended up being more efficient to just work on new ideas alone, and then bring them to a group to develop, flesh out, whatever. Sometimes even that was hard and basically everything would be done alone, and then brought to the group to consider/learn. Efficient is not even the right word, there was basically no chance of having something to work on if something wasn’t developed to a certain point alone. This situation had made me think over the years that I just wasn’t good at collaborating with people in general.

So it’s interesting to hear that others are finding this kind of collaboration unproductive too.

Some of the problems I encountered in a music context were:

• Multiple instruments in a room trying to make different things will create a lot of noise and distractions, so you kind of need to be all working on the same thing.
• Following a lead on an idea can take time, lead nowhere, and sometimes/often needs the participation of others. This can make you risk averse and passive to avoid wasting others time. This can block creativity. What has ended up happening is that some people become more passive than others and then the others feel more pressure.
• You feel a need to be working on something because that’s what you’re all there to do but there are no promising ideas. This makes it awkward and feel urgent that there be something to work on. This is bad for creativity. This also makes you just want to call it a day. it sucks.

So I ended up doing the vast majority of my work on music projects on my own, and it improved lots of things. People understood my ideas better because they were more developed, they could better judge whether it was worth it to them to spend more of their time on it and learn it, we had clearer things to work on, and more things to work on. I had less of the experience of getting stuck and calling it a day.

It also makes me realise that I haven’t really tried to make music with others in an asynchronous, remote, online-group-type way.

[Elliot]

One thing you can do is try to predict how it’ll work before testing any numbers. Then try some numbers and see if you were right.

Prediction examples: “linear increasing; solution near 100” or “exponential decreasing; solution near 0”.

Another way to make a prediction is to draw a rough graph and mark the solution. Sometimes this is quite hard but others times it’s not very hard; it depends on the problem.

With experience and looking for them, you can recognize patterns/features in the problem/equation/expression that (usually) correspond to various predictions or graphs.

[LMD]

I’m finding it hard to figure out a good way to find good problems to practise this with. After brainstorming some ways to practise it, I have continued using the Alcumus word problems. Some other ways I considered were:

• make up my own problems
• find linear equations worksheets and estimate the solutions
• research learning estimation in math and associated materials (I did this and didn’t find anything good in the short time I spent looking)

So something I’m a bit confused about is what the difference is between making an intuitive estimation, and doing the problem in my head. I find myself looking at an equation like 5x + 10 = 10x - 5 and beginning to solve it in my head with not much difficulty. But it seems like I should be doing something other than that?

As for graphing something, that’s not something I know how to do yet.

Here is some work I did:

• The value of 3x+2 is 9 plus twice the value of x+5. What is x?

• The number 1341 can be written as the sum of three consecutive positive integers. What is the largest of these integers?

• Ten more than five times x equals five less than ten times x. What is the value of x?

• In 36 years Adam’s age will be 2.5 times his current age. How many years old is he now?

• A tank is to be filled with water. When the tank is one-sixth full, 130 gallons of water are added, making the tank three-fifths full. How many gallons does the tank contain when it is completely full?

[Elliot]

@LMD

So something I’m a bit confused about is what the difference is between making an intuitive estimation, and doing the problem in my head. I find myself looking at an equation like 5x + 10 = 10x - 5 and beginning to solve it in my head with not much difficulty. But it seems like I should be doing something other than that?

This one isn’t hard to solve so you might find it easier to practice on a more complex equation where using explicit exploration steps would be more usual. But you can also examine this one without solving or simplifying it as a way of practicing.

If x is a million, which side is bigger?

If x is 0, which side is bigger?

Roughly, how large should x be for the sides to be equal? You can give a range using powers of 10, e.g. between 100 and 1,000. Can you figure out a good range estimate intuitively without any significant calculation?

There are also concrete steps that can be used to generate an estimate, which if practiced can create more intuition (and for harder problems, relying more on steps and less on intuition is common).

Does this make some sense and seem potentially useful?

@LMD

The number 1341 can be written as the sum of three consecutive positive integers. What is the largest of these integers?

If you did the calculation and got the answer 200, would you think that’s a plausible answer or intuitively be suspicious?

[LMD]

If x is a million, which side is bigger?

The right side. It means the question becomes: ~which is bigger, 5 million or 10 million?

If x is 0, which side is bigger?

The left. It means the question is just: ~whats bigger 10 or -5?

I find those easy extremes easy.

One thing I am seeing now looking at that equation is that the difference between 5x and 10x is 15, and that x should be a factor of that difference (and of 5). I didn’t really see it like that before. Maybe that’s a bit calculation-y. idk, it could be helpful technique when I estimate other things.

Roughly, how large should x be for the sides to be equal? You can give a range using powers of 10, e.g. between 100 and 1,000. Can you figure out a good range estimate intuitively without any significant calculation?

Glancing at it I think I would say it’s definitely between 1-100. For more precision I think my realisation above would be helpful. Like seeing that x was a factor of 15 means it’s between 1-15. That seems to not be significant calculation to me.

There are also concrete steps that can be used to generate an estimate, which if practiced can create more intuition (and for harder problems, relying more on steps and less on intuition is common).

That sounds cool. I’d like to learn about that. Estimating seems like something that is done a lot in daily life.

If you did the calculation and got the answer 200, would you think that’s a plausible answer or intuitively be suspicious?

I would definitely find that suspicious. I knew intuitively it had to be between 400-500.

[Elliot]

@LMD

There are also concrete steps that can be used to generate an estimate, which if practiced can create more intuition (and for harder problems, relying more on steps and less on intuition is common).

That sounds cool. I’d like to learn about that. Estimating seems like something that is done a lot in daily life.

Some techniques are:

trying some specific numbers and calculating (as we discussed earlier)

rounding numbers

deleting/ignoring smaller numbers (e.g. if x is a million, the small constants don’t matter to which side is bigger)

judging terms by order of magnitude

moving stuff so one side of the equation is 0, then estimating. (you may also want to multiply by negative 1. it’s often easier if the most important term is positive)

5x + 10 = 10x - 5

with rounding away the smaller numbers, this looks like x+10 = 10x in which case x is near 1

Or putting it into equals zero form is:

5x - 15 = 0

here we can see that x should be a small positive number

Or ignoring minor parts could give us:

5x = 10x

if you solve this exactly it has to be x=0, but what if you solve it approximately? for the two sides to be approximately equal, what sort of x would work well?

Also Big O notation - Wikipedia

You won’t understand everything on this page but could pick up a few things, like maybe the first few sentences in the “Infinite asymptotics” section would make sense for you.

[LMD]

@Elliot

Or ignoring minor parts could give us:

5x = 10x

if you solve this exactly it has to be x=0, but what if you solve it approximately? for the two sides to be approximately equal, what sort of x would work well?

Hmm, one? It seems that that way they are absolutely closer (only 5 apart). Anything more and they will still be as relatively different as they are (1:2)

[LMD]

@Elliot

5x + 10 = 10x - 5

with rounding away the smaller numbers, this looks like x+10 = 10x in which case x is near 1

Hmm I can see that rounding the -5 away could work, but I don’t see why you could round away the 5 in 5x without running into problems in general.

[Elliot]

You’re trying to make the answers too exact and calculating. For any small x (e.g. absolute value under 100), the sides will be similar, e.g. within a thousand of each other. For any big absolute value of x, like a billion, the sides will not be similar (e.g. over a million apart).

[LMD]

Right so is a better answer a range? like ‘something between 1-100’? I guess my intuition is that such an approximate answer is not that helpful, and I saw the answer 1 quickly and intuitively so answered that.

[Elliot]

@LMD

Right so is a better answer a range? like ‘something between 1-100’? I guess my intuition is that such an approximate answer is not that helpful, and I saw the answer 1 quickly and intuitively so answered that.

Knowing it should be a low number means if your answer is 500 you’d be suspicious and double check, and if your answer is 5 million you’d know it’s probably wrong.

The reason this came up is you got a wrong answer, and didn’t double check it, that I intuitively knew was suspicious.

Intuition can gain precision with practice but knowing very loose ballparks is a way to get started.

If you’re losing interest, you could go back to using the 3 section method on word problems or could move on to something else like grammar or doing the mathematical logic stuff Eternity has been doing.

[LMD]

Intuition can gain precision with practice but knowing very loose ballparks is a way to get started.

Okay. I see now that we were starting with extreme numbers as an easier initial step.

I think I am losing interest. Moving to mathematical logic seems interesting. How do you think my work with the 3 section method was looking before?

[Elliot]

@LMD

How do you think my work with the 3 section method was looking before?

OK. Didn’t really seem done but we can always revisit later if needed.

@LMD

Moving to mathematical logic seems interesting.

So you can go through the Eternity thread and try the same stuff in the same order. Don’t read ahead to avoid spoilers. (If you already read ahead some and remember some answers, just don’t do it more. No big deal.)

[LMD]

I have skimmed the first few posts in Eternity’s thread on the logic topic but mainly for any links/resources. I’ll mention if I remember anything from there if it comes up.

I started with this post here:

@Elliot

Find and do some practice problems.

Here are two types you might be able to find or create yourself:

1. Create truth table for expression like or(not(x), y)
2. Evaluate expression like not(and(1, 0))

There are multiple other ways the expressions can be formatted. Using other formats is fine.

Word problems will be later.

1. Truth tables:

2. Evaluate expressions:

if:
x = 1
y = 1

1. xnor(and(x, y), x) = 1
2. nand(x, not(y)) = 1
3. xor(not(x), y) = 1
4. or(not(x), y) = 1
5. not(and(x, y)) = 0
6. XOR(NAND(NOT(x), y), y) = 0
7. NOT(XNOR(x, y)) = 0
8. AND(OR(NOT(x), y), y) = 1

if
x = 1
y = 0

1. xnor(and(x, y), x) = 0
2. nand(x, not(y)) = 0
3. xor(not(x), y) = 0
4. or(not(x), y) = 0
5. not(and(x, y)) = 1
6. XOR(NAND(NOT(x), y), y) = 1
7. NOT(XNOR(x, y)) = 1
8. AND(OR(NOT(x), y), y) = 0

[LMD]

I’ve had trouble understanding the conditional operation ‘if p then q’ or p ⇒ q. It seems this is common with other beginners. It seems to not map well to spoken language and I’ve seen it recommended that you just think of it as a convention.

So p⇒q outputs q if p is true. That makes sense. But if p is false it outputs true. I don’t know a way for this to make sense to me. I have read that it’s equivalent to ~p v q, and I can make the truth table for that and see it, but that doesn’t seem to help me. It just seems like a fact about two operations outputting the same thing.

It seems like there should be a better way than just accepting it as a convention, and before I do I want to know if there is a better way. Do you have any advice for how to think about it?

[Elliot]

I reviewed some of the solutions and at least one truth table is incorrect.

Also, as a minor note, please use equality instead of xnor in general. They have the same truth table but equality is a more commonly used and intuitive concept.

[Elliot]

@LMD

I’ve had trouble understanding the conditional operation ‘if p then q’ or p ⇒ q. It seems this is common with other beginners. It seems to not map well to spoken language and I’ve seen it recommended that you just think of it as a convention.

I think it maps well to spoken language, so this is probably a conceptual issue for you and others, rather than a language mapping issue.

The most common spoken language versions are IF/THEN or IMPLIES. Both are commonly used phrases.

@LMD

So p⇒q outputs q if p is true. That makes sense. But if p is false it outputs true. I don’t know a way for this to make sense to me.

I can explain if needed but let’s start here:

Try making some example English sentences with IF/THEN or IMPLIES and then evaluating what the sentences mean in each scenario (each scenario = each potential truth table row). Don’t use variables.