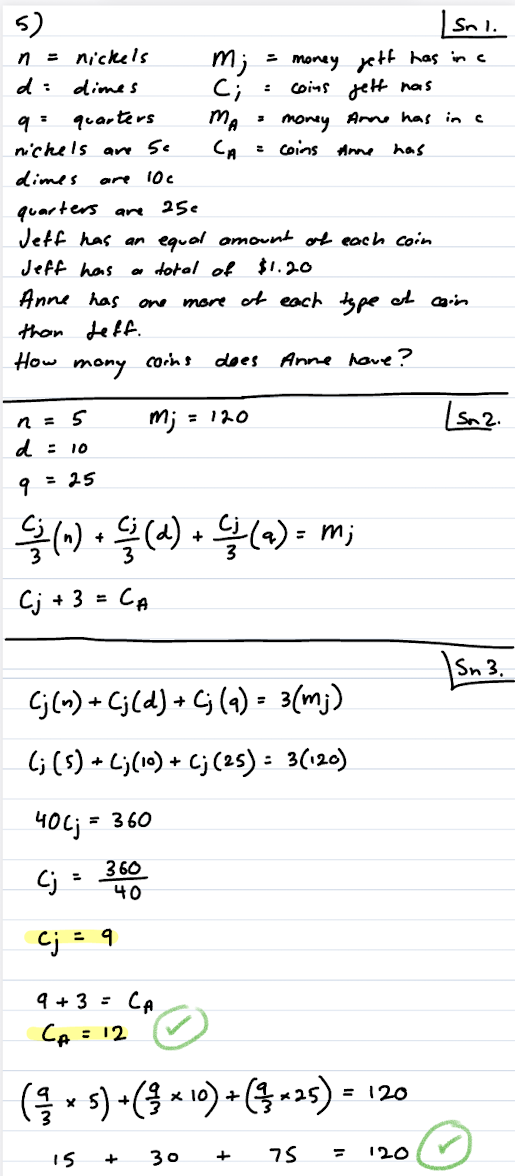You need the word “linear” for the problems.
The part you did is correct. You set up the problem well. I solved the rest based on your last step, which worked.
It’s a quadratic equation that requires techniques like factoring quadratics or completing the square. I don’t recommend looking into those.
One of the next steps I did is prime factorizing 576. I mention this to point out that prime factorizing is useful.
I noticed that website changes the numbers in the problems when the page is reloaded. I’ll leave the answer blurred for potential future use but don’t check it.
W=16, L=36
Do more linear word problems.
A hard part of this assignment was actually finding good problems. I struggled to find linear systems word problems that weren’t just painfully obvious. The more interesting ones were often mixed in with non-linear ones. So theres been a few problems that I started only to just drop and then move on, which is a bit frustrating. The following problems are from here. I’ve blurred the answers out for the sake of anyone looking for problems like this that wants to use them.
Here is some working. All problem names are my own:
Problem A:
Sisters Jane and Dane have saved 220 € in total. They are going on the trip and Jane wants to take fifth of her savings and Dane wants to take quarter of hers. If they do so, they will have 50 € together. How many euros have saved each one of them ?
Problem A working:
Problem B:
Numerator of the fraction is 2 less then denominator. If we lower the numerator of this fraction by one and we increase denominator by 3, the fraction shall be equal ¼. Determine the fraction.
Problem B working:
Problem C:
The factory has 1,440 employees (men and women). For above-average results 18.75% of all men and 22.5% of all women received the bonus. The total amount of awarded employees is 20% . How many women and how many men are employed in the factory ?
Problem C working:
Problem D:
A local train has departed from the station A at ten o’clock with the speed of 55 km/h. One and a half of an hour later an express has departed from the station B, which is 360 km far from the station A, and it went toward the local train with the speed of 130 km/h. At what time and how far from the station A will the two trains meet ?
(The problem is ambiguous about whether the trains are both heading towards each other or if only one is (like the fast one catching up with the slow one). It only says that the express train is heading towards the local train and it’s not stated or implied that the local train is heading towards station B. So they could for example be heading in the same direction and the express train is catching up to the local train. I just assumed they were both heading towards each other. I haven’t checked the answer. )
I got stuck on this one and gave up my attempt after about ~50 mins. It contains rates which I wasn’t able to wrap my head around in a reasonable time. I think I was getting somewhere but I think 50 mins was too long. I didn’t feel stumped by the problem. I could kinda sense I could do it but just couldn’t quite make it.
Problem D working:
Edit: Wrong ‘Problem B’ image uploaded. Changed to correct one.
For D, it’s ambiguous but based on familiarity with other problems they want the trains to go the same direction with the faster train catching up to the slower train.
Try it that way. If you’re still stuck, brainstorm a list of variables that might be useful. Or just make some useful equations by assuming you have all the variables that you’d need for them. Or try creating and solving easier variations of the problem with different numbers.
Okay so the way I did this was not really via the 3 section method. In an attempt to just think through the problem and write down my thoughts I ended up solving it. I didn’t really end up with a pair of equations. Idk, I’m not sure what to think.
When I checked my answer against theirs it was wrong so I made the appropriate numbers negative and checked to see if it gave the right answer and it did. So they intended for the problem to be for trains heading towards each other, and my answer for one train following the other would’ve been right.
Here is my working:
Here’s my plain text file for setting this problem up. For 2-3 character variable names, read characters after the first as subscripts.
A local train has departed from the station A at ten o’clock with the speed of 55 km/h. One and a half of an hour later an express has departed from the station B, which is 360 km far from the station A, and it went toward the local train with the speed of 130 km/h. At what time and how far from the station A will the two trains meet ?
sa is speed of train a.
d = distance from station b. If you imagine the trains are going straight north, then that’s the south-most point used in the problem.
da0 is distance of train a at time 0. Time 0 is the moment when the first train starts moving.
dat is distance of train a at time t.
t is the solution time (hours since time 0), when the trains meet.
distance = speed * time
Section 2:
(blurred so you can try it yourself first if my section 1 gave you any ideas)
sa = 55
sb = 130
train_b_late_start_hours = 1.5
t > train_b_late_start_hours
da0 = 360
db0 = 0
dat = da0 + sa*t
dbt = db0 + sb*(t-train_b_late_start_hours)
dat = dbt
When you’re having difficulty, you should write variable names out more fully. Examples:
sb = speed_of_train_b
dat = distance_of_train_a_at_time_t
or
dat = distance_from_station_b_of_train_a_when_trains_meet
You can do the whole problem using only long, descriptive variables so it’s easier to understand what things mean. That’s wordy and may seem unusual for math, but it’s one of the standard styles for programming.
Rewrite my setup using long variable names, then solve for the time the trains meet.
I didn’t include finding distance from station A, so you can add that in too.
Afterwards, modify the setup for train A going towards station B instead of away from it, then solve that version. Make a list of what modifications were needed and share any comments you have on what that list looks like.
Okay, I haven’t looked at your section 2 and I’m attempting it. Am I right that your section 1 variables and the constants in the problem are all that are needed to calculate the time t?
No I just gave enough information to understand section 2
Try some without unblurring this, but if you need more info here is section 2 with only the left sides of the equations.
sa =
sb =
train_b_late_start_hours =
t >
da0 =
db0 =
dat =
dbt =
dat =
OK. So I unblurred the part with the left sides of the equations because I got stuck. I didn’t check your complete section 2 until I did mine though.
I really struggled with this and I don’t know why yet. I think I was second guessing myself a lot. Maybe I wasn’t focusing enough on my understanding of the problem and my ideas on how I could solve it, and was focusing on trying to interpret or decipher the clues given to me. (That’s why I asked that clarifying question before) And also I think I was assuming a lot about what kind of result I should get. Like I thought I should have two linear equations with two unknowns each.
I also didn’t find writing out the long variable names in the equations very helpful. I found it made some things harder. Also hard to like, see the equation when the operators were so far apart. Something I did find helpful (which is similar) was writing out in words what each part of an equation meant for example:
sb(t-1.5) = distance travelled by b in 1.5 hours less than t
My Section 2 (based on your left hand side):
sa = 55
sb = 130
train_b_late_start_hours = 1.5
t > 1.5?
da0 = 360
db0 = 0
dat = da0 + (sa * t)
dbt = db0 + sb(t - 1.5)
dat = dbt
da0 + (sa * t) = db0 + sb(t - 1.5)
My Section 3:
360 + 55t = 0 + 130t - 195
555 = 75t
555/75 = t
t = 7.4
Finding the distance from station A that the trains meet:
sa * t = distance of train a from station A when the trains meet
55 * 7.4 = 407km
OK
Section 2:
sa = 55
sb = 130
train_b_late_start_hours = 1.5
t > 1.5?
da0 = 360
db0 = 0
dat = da0 - (sa * t) - changed
dbt = db0 + sb(t - 1.5)
dat = dbt
da0 - (sa * t) = db0 + sb(t - 1.5) - changed
Section 3:
360 - 55t = 0 + 130t - 195
555 = 185t
555/185 = t
t = 3 hours until trains meet
sa * t = 165km from station A
list of modifications:
dat = da0 minus (sa * t) - because train a is travelling in the opposite direction, so the distance it travels in time t is negative.
Small thing: you used the number 1.5 instead of train_b_late_start_hours a few times. The basic downside of that is the number isn’t self-explanatory.
Note: this is a system of linear equations where you’re using around 7 equations. But it’s not actually much harder to calculate than a system of 2 linear equations. That’s related to the equations mostly being simple and most of them having a low number of variables.
Switching the train direction doesn’t take many changes when the problem is set up well.
da0 + (sa * t) = db0 + sb(t - 1.5)
IMO this goes in section 3, not 2. I consider it a calculation based on equations from section 2.
Anyway, that’s good. Try some more word problems and hopefully this will be helpful for future problems.
Gotcha.
Here are some simple ones that I did yesterday with times. I got the problems from here in Eternity’s tutoring thread. I haven’t checked the answers yet, and there’s one more I need to do when I’ve got time. I haven’t done another rate one yet but I’ll find some more asap.
- A girl is half as old as her sister and is also two years younger than her brother. If the sum of the three children’s ages is 34 years, what is the product of their ages?
- In a certain school, 2/3 of the faculty are women, 1/4 of the men on the faculty are married and the other 9 men are bachelors. How many faculty members are there?
- John divided his souvenir hat pins into two piles. The two piles had an equal number of pins. He gave his brother one-half of one-third of one pile. John had 66 pins left. How many pins did John originally have?
- If 20 is added to one-third of a number, the result is the double of the number. What is the number?

All my problems are from Alcumus. You seem to have used it before:
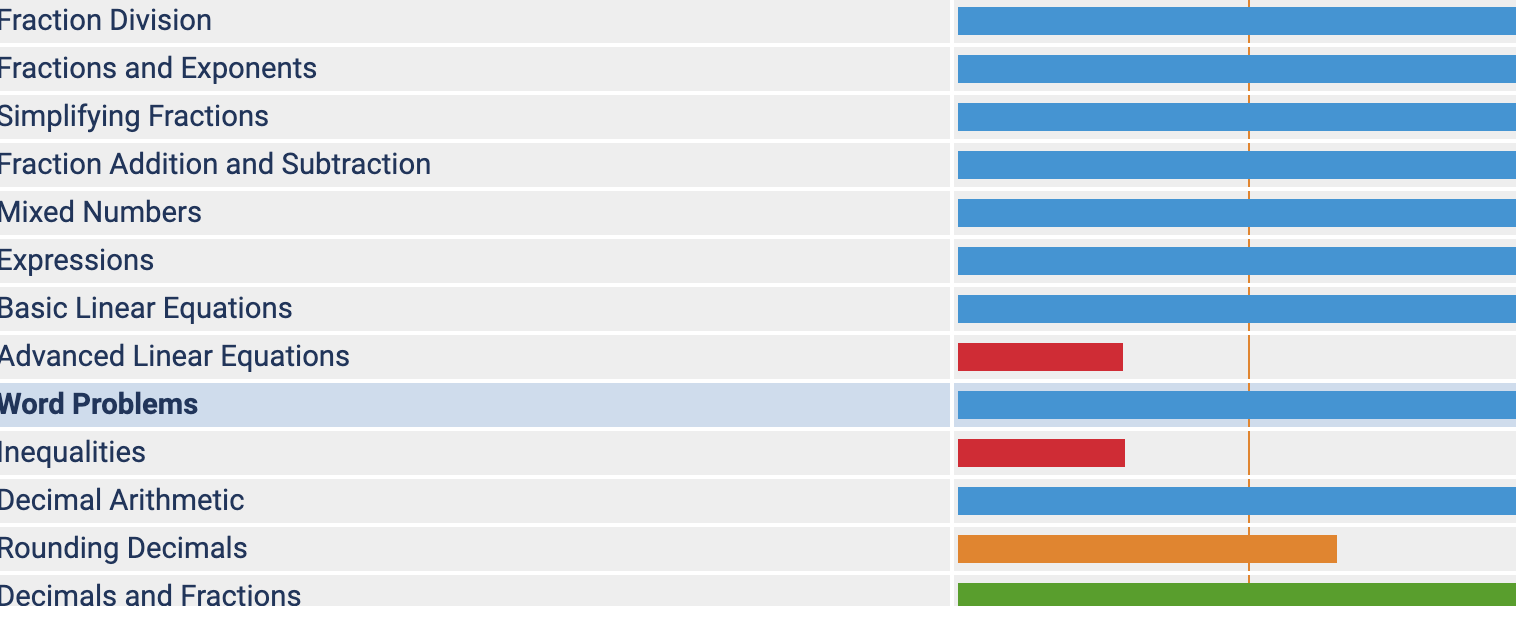
Where it says focus, you can click on change focus, and choose a topic area to focus on.
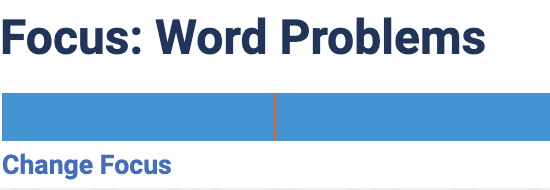
If you get enough right it will move you away to another topic but you can always just reset it back to word problems.
EDIT:
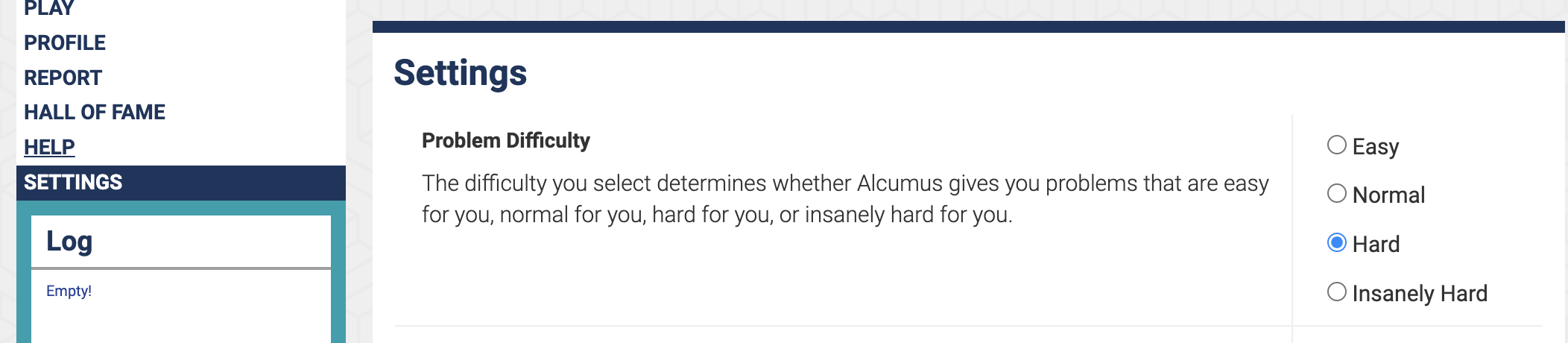
They also have difficulty selection in the settings:
After arriving at an answer for 4, you didn’t confirm it by checking it with the original problem. Do that check.
Thanks for that. I had been meaning to ask you where specifically to find them. I have used Alcumus. But I couldn’t find linear systems word problems when I looked. But I see now I was just looking under Algebra (where two variable systems are) and not Prealgebra too. The ones I did find under Algebra were too hard.
Woops yeah 60/5 is not 30, but 12.
So there are 3 issues here. The arithmetic error. Why didn’t you check your solution for that one? And also more intuition about the numbers and problem would help catch errors like this. Like if you read the problem, do you intuitively know if the solution should be more or less than 20?
I’m not sure.
One thing was that I was focusing more on sections 1 and 2. I was also doing these in a short window of time before I had to leave for work, and I wanted to get through the 5 I had selected. Problem 4 seemed to me to be very short and not offer much to practise re sections 1 and 2, so I might’ve been keen to just move on to the next problem (which I didn’t end up getting through in time). That could be why I skipped checking it.
But, I probably also just intuitively thought that was the right answer and so not thought I should check it. But using intuitions about when to check your work that rely on intuitions about whether your answer is right seems problematic though now I say it.
My intuition would say that the ‘result’ (double the number) was over 20, but not necessarily that the number (n) was more or less than 20.
Sorry as in, the result of adding twenty to a third of a number is more than twenty.