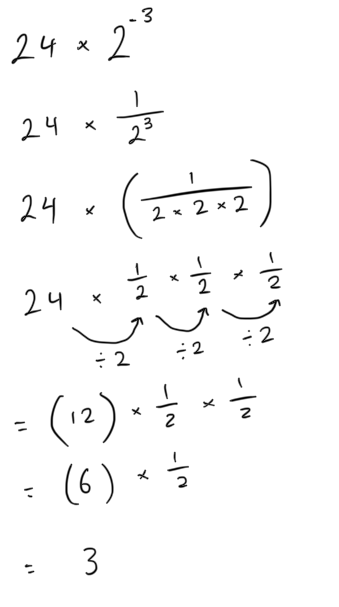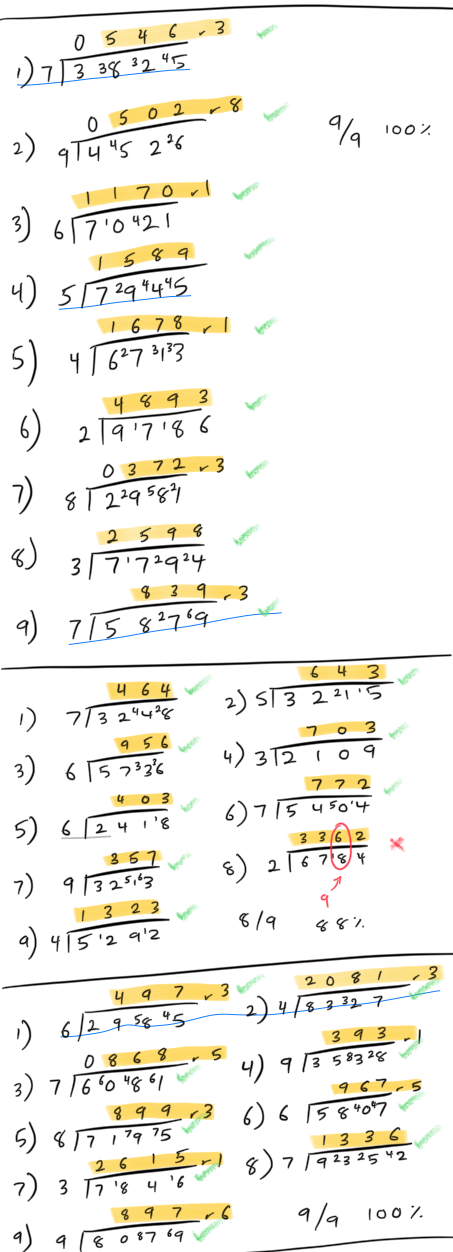hmm, not really. Something to do with grouping maybe? so that 4 x 5 would be 4 groups of 5, or vice-versa? That doesn’t seem that different to repeated addition though.
What if you multiply by 1.3? Repeated addition doesn’t work as cleanly as with integers.
Hmm. I spent about 5-10 thinking. I couldn’t come up with anything. Its something that works more cleanly with fractions and decimals?
Oh okay, that makes sense. I’ll have a read.
What are subtraction, division, multiplication by a negative number, roots, and exponentiation by a negative number?
Subtraction: repeated use of predecessor.
Division: multiplication by reciprocal (multiplicative inverse)
Multiplication by a negative number: repeated addition of a negative number
Roots: the factor of a number which if raised to the power of the root gives that number
Exponentiation by a negative numbers: reciprocal of the positive exponent
–
I didn’t do research on this. I just tried to describe the concepts from my exisiting understanding.
If you want to subtract 3, 5 times, what do you use?
If you want to divide by 4, 7 times, what do you use?
If you want to subtract 3, 5 times, what do you use?
multiplication by a negative number
-3 x 5
If you want to divide by 4, 7 times, what do you use?
Exponentiation by negative numbers
So exponentiation by negative numbers, is repeated division?
Yeah, but I’d do it the other way. In general, with lots of operations, you can view the first number as the starting point or thing to use, the operation as telling you what to repeat, and the second number as telling you how many times to repeat it.
So I’d write 3 * -5
Which means we’re going to repeatedly add 3’s. How many times? -5. Adding it less than 0 times means taking it away – the inverse – so it would cancel out or undo adding it positively the same number of times. (You can think about how this relates to multiplying by something a negative number of times.)
You can also have a starting point you want to repeatedly subtract from, e.g. solve: 50 + 3 * -5
I’d read -3 * 5 as saying to add up five -3’s, not to use subtraction. That’s similar and gets the same numeric result.
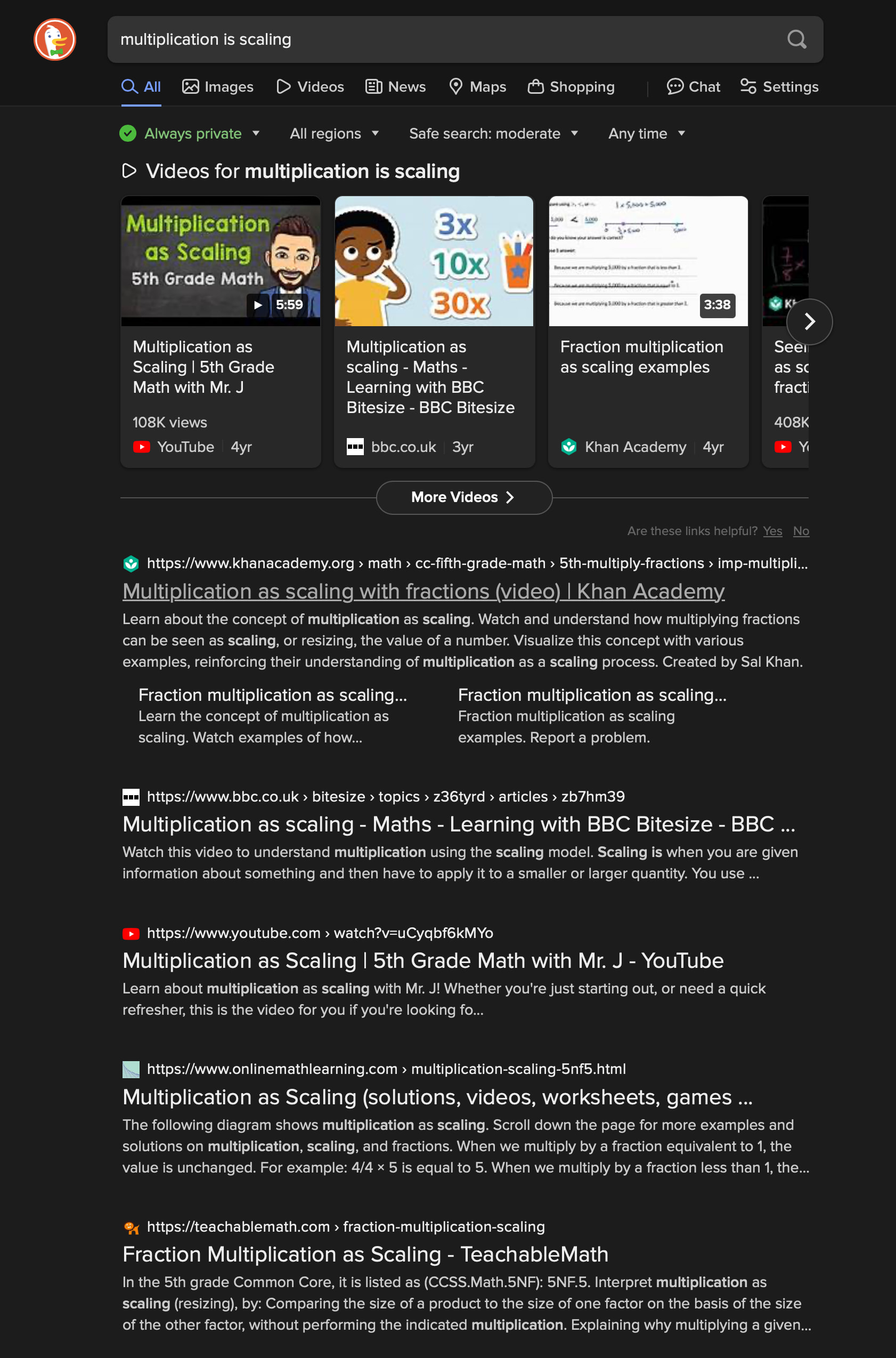
Try it out. What is 24 * 2^-3? Write out the steps the long way and think about what is being done to the 24.
So next let’s look at division then roots more. For division, what do you do to divide? What are the steps? What is the goal?
So with e.g 6 / 2 I’d read that as: what number is 2 equal parts of 6? For a lot of division, I can figure out the factors myself, or I’ll use a calculator. But am not sure what the operation is doing. Like I don’t know how a divide function in a calculator works.
In this case, you could get the right answer by subtracting 2 until you get 0 and counting how many subtractions it took. But if you are dividing by a number that isn’t a factor then you get a remainder. So I’m unsure if division can be characterised just as repeated subtraction.
That’s why I thought characterising it as multiplication of the reciprocal made more sense to me. But, wouldn’t a calculator still have to use division to find the actual value of the reciprocal to use it in a function?
Yes, that is one of the main ways to understand division. It involves repeated subtraction, but it’s also different because the answer is the number of repetitions, not the number you get by subtracting.
There are multiple ways to handle remainders. One ways is to give two answers: the quotient and the remainder. Other options including rounding down or giving the answer as a mixed number.
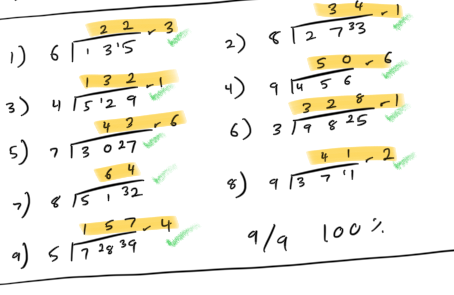
Instead of having a remainder, you can also calculate a decimal answer using short or long division. So let’s have you practice short division.
Try some with remainders first.
Then, for decimals, you basically write .000 on the end of the number and then continue the same algorithm into the decimal places.
Also, practice some long addition, subtraction and multiplication.
Spent ~1 hour. Did four worksheets on division problems with remainders. 36 problems total with one wrong so ~97% accuracy.
I can see how you can express the remainder as a mixed number now and I tried extending the number with .000 and can see how that allows you get higher precision.
Also, practice some long addition, subtraction and multiplication.
Cool
A log of what I did yesterday:
Long multiplication worksheet. 8/12 = 75% accuracy. I can account for two errors being a method misunderstanding which I easily fixed. The other two are basic addition errors. Going to go practise long addition before I do more multiplication.
Long addition with regrouping: 1hr 23mins. 87/88 problems correct. ~98.8% accuracy
Back to long multiplication. 16/20 problems correct. 80% accuracy. Most errors are basic times tables errors like confusing 8 x 4 and 6 x 4. I’m going to revisit my time tables under 10 before proceeding with long multiplication.
6, 7 and 8 times tables seem harder than others to me. I went over those here:
8 times tables 143/144 in 5 mins, ~2 seconds per question ~99.3% accuracy.
6 times tables 161/162 1.85 seconds per question ~99.3% accuracy
Today:
Did a 2 digits by 2 digits long multiplication worksheet this morning. 16/20. All caused by single digit/times tables errors.
Did about 1hr of times tables work, focusing on 6, 7, and 8 times tables.
Did a second 2 digits by 2 digits long multiplication, got 17/20 but with no multiplication errors. Only errors were from forgetting to add the zero to the second line when multiplying the digit in the tens column. I think this is because I was focusing so much on the single digit multiplications that I forgot some of the long multiplication method. I think if I slow down I will be able to get 100% next round.
Did a third 2 digits by 2 digits long multiplication, 20/20 100%. Focused on the previous issues. Planning to do a few more of these at 100% before going up to 3 digit by 3 digit long multiplication.