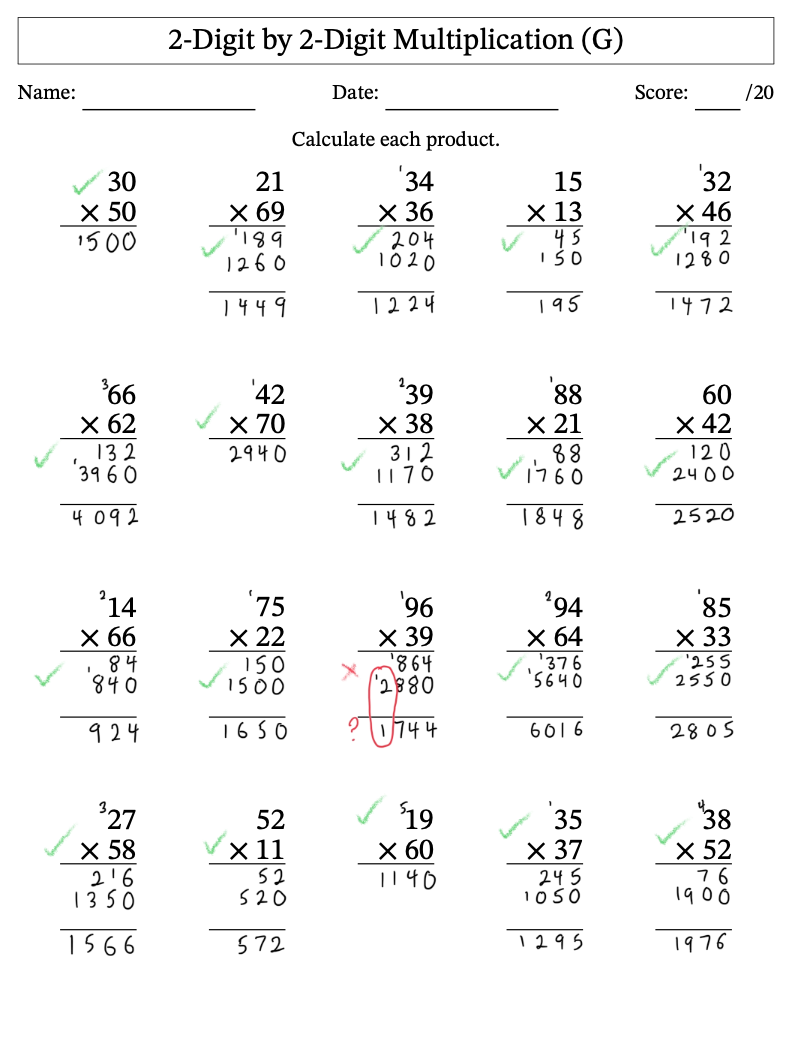
My fourth long multiplication worksheet: 20/20 correct.
Typing quotes: 61.10 WPM 98.53%
Typing.com 67wpm 99%
https://monkeytype.com/ english 200 no punctuation: 82WPM 100%
Over the last few days I’ve been practising slower and evenly to a metronome because I noticed that my speed was very uneven. I think it is helping but it’s taken me a few steps back at first. I am hoping for better results from it soon. My times are only marginally better and no real increase in accuracy on this weeks tests.
Spent ~2hrs on multiplication today. Into total out of 100 problems, 95% accuracy. Did some times tables revision too.
2 by 2 Long Multiplication - 95% (19/20)
2 by 2 Long Multiplication - 95% (19/20)
2 by 2 Long Multiplication - 100% (20/20)
3 by 3 Long Multiplication - 95% (19/20)
3 by 3 Long Multiplication - 90% (18/20)
I think your accuracy would go up if you did and wrote out more steps. Multiplying 1 digit by 3 digits in your head is not necessary.
For 2 digit by 2 digit multiplication, do you know how to do it as 4 single digit multiplications and add those?
Yes I’ve been doing all of these (including 3 by 3 ones) as a series of single digit multiplications, and then doing long addition on the products of those to get the final product.
I haven’t been doing that. Maybe the worksheets I’ve shared give that impression somehow? But it’s all repeated single digit multiplication.
I’m not sure how to break this down further apart from switching to doing more single digit multiplication (practising times tables) or breaking down the single digit multiplications into repeated addition (which I’m unsure would lead to less errors)
Are you writing on something else or keeping track of some numbers in your head? For the 3 by 3 problems I see 3 numbers written down and added, not 9.
This is approx the method I’ve been using. You get 3 numbers to add together, not 9. It is still single digit multiplication but it does incorporate addition into it by carrying digits over to the next column.
I can see that there is another method which leaves all addition to the last step which would give you 9 numbers to add for a 3 by 3 multiplication. That sounds like what you’re referring too. I think that would be good to try to separate those phases. I’ll try that today!
Actually at 1:40 in that second link they talk about the ‘expanded’ method which is the one I’m currently using. It’s a better illustration than the first link.
edited.
Wait sorry, I meant 1:40 in the second link. I’ve edited the above post to reflect that.
Sorry, to answer your question: no I’m not writing on something else or keeping track of numbers in my head. All my working is on those sheets. Some of the superscript numbers I erase so i can write new ones when I e.g move from the 1s to the 10s column.
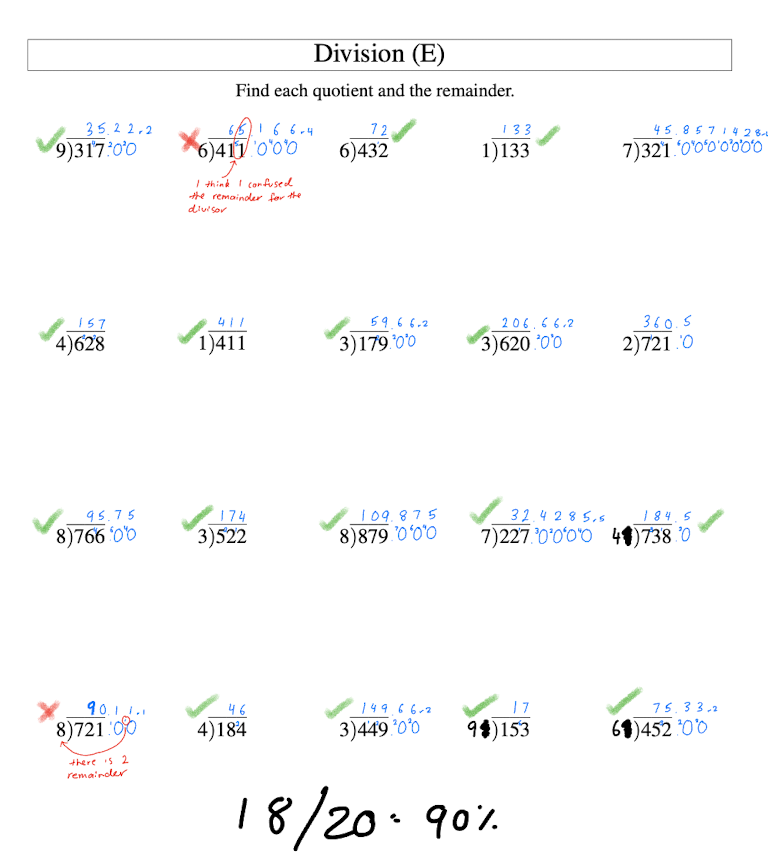
I spent 1.5 hrs today on one 3 by 3 long multiplication worksheet. I used the new, longer method mentioned above. I found it slower which is to be expected. But I still got 19/20 which is a bit frustrating/disheartening. My error was one long addition error where I read 4 + 1 as 4 * 1, which I think was a lapse in concentration.
I am not really looking forward to the prospect of more days practising long multiplication, and I’d like to move on.
19/20 with just one concentration error is OK. Here are assignments:
- Explain the additive, multiplicative and exponentitive identities.
- Explain the base 10 number system.
- Short division with decimals.
- Look into unit conversion.
OK. I’m doing all these assignments without researching.
The additive, multiplicative and exponentitive identities are numbers that the respective addition of, multiplication by or exponentiation of preserves the identity of the number operated on.
The additive identity is zero. Zero can be added to any number without changing that number.
The multiplicative identity is 1. Any number can be multiplied by one without changing that number.
The exponentitive identity is 1. Any number can be raised to the power of 1 without changing that number.
time: ~20 mins
The base of a number system is a convention for the way numbers are named and written. A base 10 number system groups numbers into 10s and powers of 10. This is reflected in how we name numbers e.g tens (10^1), hundreds (10^3), thousands (10^4), etc. and also how we write them out: another digit is added for each power of 10 e.g 10, 100, 1000, etc. (also negative powers of 10 for expressing numbers smaller than 1 i.e decimals.)
The base of a number system does not effect the underlying mathematical relationships between numbers. The same math can be done with a base 2, 3, 5, 12 etc. system.
time: ~20mins
typo?
Oh, yes that is a typo thanks. I meant: tens (10^1), hundreds (10^2), thousands (10^3).
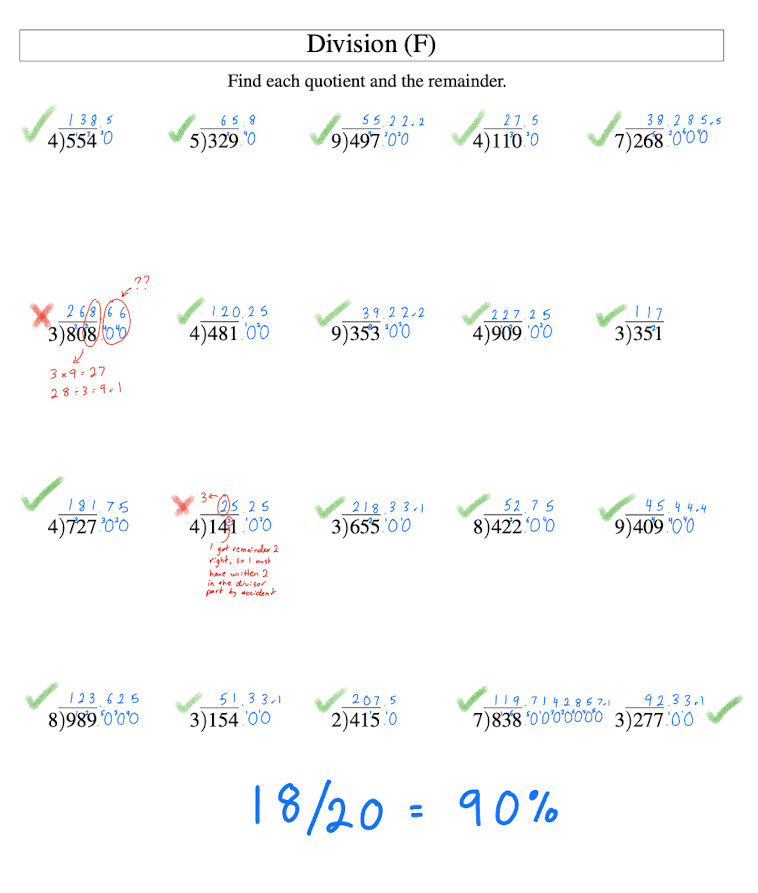
Spent 1hr 45min total doing 100 short division problems. 93% accuracy. 2 of my errors were from accidentally writing the remainder where I was meant to write the divisor. 4 were errors involving multiplication with 9.
The last one i did i wrote out all the multiplications so they weren’t just being done in my head. That seemed to solve the multiplication problems. But I still made one error of writing the remainder where the divisor was meant to go.
Here is my working:
OK. Let’s still go on to unit conversion next and see how that goes.
I did some investigation into unit conversion, and made some notes/self-explanation.
Unit conversion
The key concept of unit conversion is: changing the unit that a quantity is expressed in while preserving that quantity.
What does that mean and how can we do that?
Quantities are expressed in units. We express a quantity in units by expressing it as the product of a number and a unit. So the distance 600m means: 600 x m(one meter). It tells us what amount(600) of units (meters) our quantity(distance/length) is.
Unit conversion relies on the fact that 1 is the multiplicative identity; the fact that any quantity multiplied by 1 remains the same. 1 can be written in many ways, and this allows us to change the unit a quantity is expressed in while preserving the quantity.
We can express a quantity as an equality between two different units:
- 1000m = 1km
Since 1000m and 1km are equal, dividing one by the other give us 1.
- 1000m/1km = 1
and - 1km/1000m = 1
These are conversion factors. Since these conversion factors equal 1, we can multiply a quantity we want to convert by them without changing the quantity. Rearranging the expression so that the original units are cancelled, and the units we want to convert to remain, allows us to convert between units.
OK I think it’s time to revisit Multi-Factor Decision Making Math and look for math you don’t understand.