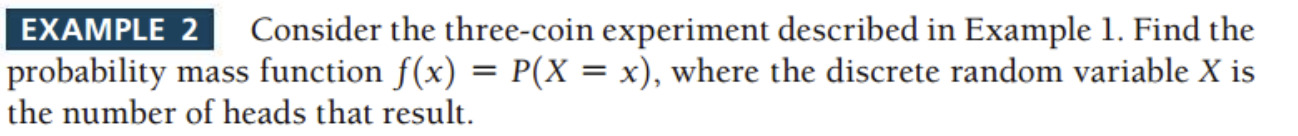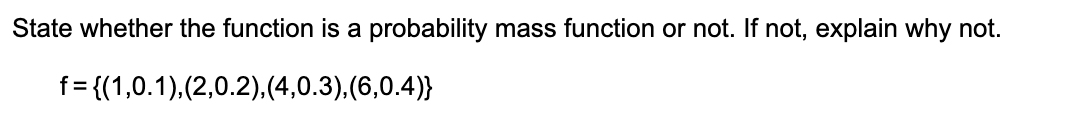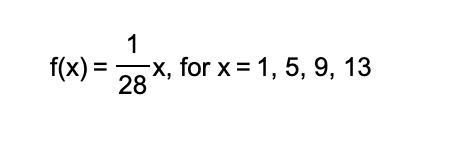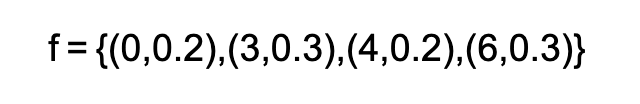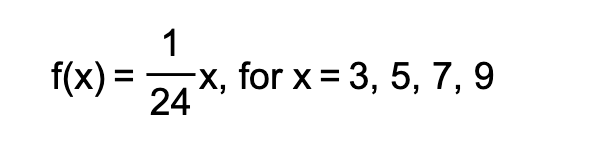I decided to restart my college classes. I’m starting off with just one class soon, called “Math for Business Analysis”. I figured I’d share about it here. I could maybe get some feedback on some stuff but I’m not too expectant and getting a crazy amount of help for the math. Its more so to share what I’m learning, maybe get some help, and to share some stuff in real time about a college class online.
The math covered:
From Section 6.1 Functions of Several Variables
A real-value function of f of x, y, z, … is a rule for manufacturing a new
number, written f(x, y, z …), from the values of a sequence of independent
variables (x, y, z, …) .
A real-value function is a rule. It’s a rule for coming up with/outputting a number. You follow the rules and you get a number. The output is based on the values of independent variables.
The graph of the function f
of two variables
consists of all points of the form
(x, y, f(x, y)) .
The graph of a function that has two variables consists of points coming from both variables and their output.
Hmm. Is the graph of a function that has one variable this then: (x, f(x)). I think I’ve seen it like that before. So graphs of a function consist of the points going into the function and the output.
In 3d space, there are 3
mutually perpendicular axes:
• x-axis (extend to the front)
• y-axis (extend to the right)
• z-axis (extend upwards)
Huh. That seems so odd to me. I’ve never exactly dealt with space before, but just going off of how an xy coordinate plane looks y just felt like the part that extends above.
So x-axis is in front and behind me
y-axis is to my right nad left
and z-axis is above and below
In 3d space,
there are 3 coordinate planes:
• xy-plane where z = 0
• xz-plane where y = 0
• yz-axis where x = 0
So a plane is when the graph looks flat? I guess? Also what does the coordinate have to do with anything here.
From Plane (mathematics) - Wikipedia :
In mathematics, a plane is a two-dimensional space or flat surface that extends indefinitely.
Ok. So I get what the plane here being referred to is. What’s the coordinate? From Gemini:
The term “coordinate plane” refers to a Cartesian plane, which is a two-dimensional plane defined by two perpendicular number lines called axes. It’s called a coordinate plane because it allows us to locate points by using coordinates, which are pairs of numbers that specify the point’s position relative to the axes. The plane is named in honor of René Descartes, who developed the system.
Hmm. It seems Gemini highlights the part it thinks I’m looking for. Neat.
Ok. That makes sense . So coordinate planes are planes that have coordinates. When you have three dimensional place you can form three different coordinate planes.
If we hold a variable constant,
the graph of the set of points is a plane.
Hmm. So the coordinate planes are when the variable being held constant is 0. At least thats what it seems like so far. Why is that? Hmm seeing this:
My thought process is that you could do a coordinate plane from there. Its just when doing coordinates I guess you assume its 0 otherwise you would list that third coordinate even if its a constant.
The graph of a function f of
two variables is the set of
points (x, y, f(x, y)) in three
dimensional space where we
restrict the values of (x, y) to
lie in the domain of f.
I forgot what a domain is. Let’s see. From Domain of a function - Wikipedia :
In mathematics, the domain of a function is the set of inputs accepted by the function.
Ok.
This course sounds like it would have algebra and more as prerequisites. But you recently said you wanted to work on a prealgebra book. So I’m a bit confused; if you think you know algebra well enough to build beyond it, why work on prealgebra?
Hmm. Let’s see. To start off with, I didn’t know what math this class covered. I did know it was built on calculus (I already completed a calculus class before).
Did I not share before that I did math up to Calculus? I feel like I have. Maybe I’m misremembering, but I think it was in call before starting tutoring where you asked a lot of questions.
The reason I want to work on the pre-algebra book is because I don’t think I know the math that well. Or put differently, from Cycle Between Learning Critical Fallibilism and Its Prerequisites :
E.g. the way people think about arithmetic, algebra or grammar is good enough to pass school tests but not good enough to build up to advanced philosophy. Improving those basic skills to atypically high quality standards is relevant to CF even though it’s many layers separated from CF.
I think I know the math well enough to do this math for school, but not well enough for CF. This is the only math course for my degree that I can tell. Well that and Calc 1 I guess which I already took. So I’m not too worried getting far in math classes I don’t understand well. Plus, skimming through the material I think the Professor is definitely teaching in a way that I can get the answers he wants on a test but not really teaching it for high quality understanding/learning. So I think I should be fine.
Oh yeah I guess the other thing to your question: I’m not trying to necessarily build up my math skills. I recently changed my major to Business (Law) (the parentheses is in the name of the degree). I’ve heard Business is an easy major. So I figured an easy major with a focus in something I’m really interested in will make getting this degree easier. I’m only really pursuing this degree for law school after all. So my goal with this class is just to finish a pre-requisite.
So I watched two of the lecture videos so far and one I’m realizing is that the lectures are just reading off the slides word for word. I wonder what the point is? Maybe for people who don’t like reading? Also, it didn’t help me with material but I have had better success at understanding stuff from listening as opposed to reading,
Maybe one reason the lectures aren’t too helpful is that it covers math I’m already familiar with? Or, in other words, I’m comfortable reading the material on my first try due to familiarity.
From Section 6.2 Partial Derivatives:
The nth partial derivative of f
with respect to x is the
derivative of f with respect to x
when all other variables are
treated as a constant.
and
The nth partial derivative of f
with respect to y is the
derivative of f with respect to y
when all other variables are
treated as a constant.
Huh. So I thought treating all the other variables was a shortcut. Or, put differently, I thought multivariable derivatives would involve some complicated method to find the derivative in relationship to two variables and the partial derivative stuff is a simple thing we’re doing for this class, but after googling it seems pretty standard.
Hmm. So I went through the problems and they seem pretty easy. Idk what the point is of doing partial derivatives (but truth be told I don’t even understand what a derivative really is, yet I was one of the best math students in high school definitely could be a big fish in a small pond situation but just wanted to share that point) but the hard part just seems to be keeping track of when a variable is treated as a constant and when its being treated as a variable.
Students expect lectures. Lectures are generally advertised as part of courses. Teachers are told by their bosses to give lectures. I imagine poor lectures get a lot fewer complaints than no lectures.
That makes sense. Also I do think there was a part of me that found the lectures bad because of previous familiarity with some of the stuff taught. I watched a different lecture on some math I was less familiar with and I found it a bit more helpful (even though it was still kinda just reading off slides).
I wonder: I find it harder to go over stuff I feel like I already know. Is this normal or good? I think its normal. I don’t think its good. Even though I was very familiar with some of the math already covered (well familiar enough to do the problems at least) there was still some stuff I forgot. I found it annoying to relearn the stuff I missed because I felt like I already knew it.
This also happened when we went over word problems. I don’t think I shared much of how I felt at the time but I think I was very annoyed at doing the word problems because I had a feeling that I knew how to do them, even though I failed at them a lot and the stuff we worked on did help.
Should I try to make myself recognize that I still have stuff to learn? I wonder.
Yeah. Normal but not good. People often overestimate their knowledge and this attitude can get in the way of improvement long before they reach total mastery.
Even if you know it, more practice and exposure can be good.
Also this attitude is incompatible with being a great teacher. A teacher should find the material interesting to review, not be bored by it. For example, I often find grammar analysis interesting instead of being bored because I already learned grammar.
I find it strange that people can think they already know stuff, and therefore not want to learn it more, when they’re already making frequent errors. That doesn’t make a lot of sense to me. It’s common though.
Why “make” yourself recognize it instead of just recognizing it?
There are lots of things you could do. Better understanding your infinite ignorance and the limitations of your knowledge, both in general or for particular subjects, could help. Having different ideas about satisfactory error rates could also help.
I find that having high quality knowledge of standard fields, well-known fields is an under-explored way of making significant intellectual discoveries. There’s a lot of competition to try to come up with fancy new advanced stuff but just being better at more basic stuff like arithmetic can lead to progress that not many people are even trying for Multi-Factor Decision Making Math I think this applies in science and other fields too: more progress could be made if more people understood the topics from school better, and applied them better, instead of trying to build advanced new stuff on them.
10.1 A Review of Sets:
Apparently I should know about sets already. I do know this class builds on other math classes I’ve taken and I don’t remember them covering sets. I guess I’ll just figure it out while doing the problems.
Hmm. So this is the first time I’m told to read the textbook. Ok I’ll see what it has about sets.
From the textbook:
We often consider collections of objects in everyday life. For example, the students
in your class, the letters of the alphabet, the members of your family, and the positive
even integers are all examples of sets. The objects within a set are the elements or the
members of the set
Sets are collections of objects and the objects in a set are formally called elements or members of a set. Ok. I already knew that.
a set may be written in two ways: using the
roster method, in which the elements are listed, or using set-builder notation, in which
the elements are described.
So with Harry Potter books:
roster -
H = {Harry Potter and The Chamber of Secrets, Harry Potter and The Prizoner of Azkaban, etc.}
set-builder -
H = {h|h is a book in the harry potter series}
Hmm. a.) has no solution and b.)’s solution is x=-1. Do I write the circle with a line by itself or in brackets to denote an empty set? b.) should just be {-1}, Let’s see:
Ok. So just write a line with a circle. Ahh. Out of habit I just assumed we were solving for when x is equal to 0 for b.).
Hmm. So I’m a bit confused on what it means by saying that the “universe is assumed to be the set of all of the real numbers” because a universal set, according to the textbook, is:
A universal set (also called a universe), denoted by U, is the set of all elements
in the context of a situation.
So is it saying that all of the real numbers is the set of all elements in the context of algebra and calculus?
a.) true, 3 is an element in the set
b.) true, {2, 3} is a subset of the following set
Let’s see:
Ok I was wondering about that with a.). So if it has brackets around it, it’s a set. An element of a set should be written as is I guess.
The organization of elements in a set doesn’t matter, but repeated elements are ignored. That’s a bit confusing. Why is that? Let’s see: a set with all of your classmates but two of them are named John. I don’t think its talking about something like that. The two Johns are different, but similarly named, elements. I guess if we have a set like all of your classmates name and a name pops up multiple times it doesn’t change what the set represents? Having the same Samantha show up five times in your set doesn’t change the fact that the set represents your classmates and that their is only one Samantha in there.
Ok. I’ll stop there for now.
Hmm. I do remember enjoying going over stuff when helping my brother and my friends with math problems in the past. I remember being out of high school for a bit and not having touched calculus for a while. Reviewing Calculus to help teach my brother was fine but reviewing in and of itself usually isn’t. Maybe its because I’m doing it for the goal of teaching and that makes it fine? Versus if I just review it in and of itself I feel like its a waste of time because I think I already know it?
Well I guess its because I kinda do recognize it but I don’t know why its not being recognized(?) in my subconscious. Like when we did word problems, I knew I was bad at them and so I didn’t complain about doing them. I recognized I had stuff to learn about doing them (and still do now). Yet the whole time I still felt like I was wasting my time doing something I already knew.
That makes sense. Also I wonder how much better some of the advanced stuff could be if the the basic stuff was understood better.
You said x=-1 so x wasn’t equal to 0 in what you did.
Ahh. Woops. I meant I was used to solving quadratics where you find the x-intercepts. Which is when y is equal to 0, not x. I kinda treated (x+1)^2 = x^2+2x+1 as them giving me the factors for the quadratic equation for some reason and assumed we were looking for the x-intercepts.
Some more notes from the chapter on sets:
If A is a subset of the universal set U then the complement of A, written A’ (read A prime?), is the set of all elements that are not A but are in the universal set.
A union between sets is like and/or. A union between set A and set B includes all elements in set A, all elements in set B, and all elements common to both. A union involves them joining together it seems.
An intersection between sets is like and. The intersection between set A and set B are all elements shared between set A and set B.
If there are no commonalities between set A and set B then the sets are considered mutually exclusive. Or, in other words, if the intersection between set A and set B is an empty set then the A and B are considered mutually exclusive.
Cardinality of a set refers to how many unique elements there are in a set. Hmm. I’m a little unsure if this understanding is correct but I guess its not important. I say unique because repeated elements are ignored when counting for cardinality. I just don’t know if unique is the right terminology here. Probably just overthinking it.
So it seems cardinality is denoted by n(set_name).
n(A) = 4, n(B) = 5, A U B = {m, a, t, h, e, l, e, m, e, n, t} = n{A U B} = 7, so no the cardinality of the union of two sets does not necessarily equal the the cardinality of the two sets added together.
Inclusion-Exclusion Principle:
The cardinality of the union of two sets is equal to the cardinality of the individual sets added together minus the cardinality value of the intersection of the two sets.
Thats it for sets stuff. Part of the reason I read the textbook is because the professor said there would be no lectures and to read the textbook if needed. I liked reading the textbook but I wonder if its because I was already somewhat familiar with the basics of sets already. I may try using the textbook for subsequent sections.
Using the textbook again. 10.2 Theoretical Probability Notes:
In probability, an experiment can be any action that has clear results, and those results
are called outcomes. Each performance of an experiment is known as a trial.
What would be an action with an unclear result?
In experimental probability, an experiment is performed many times, and the prob-abilities of the outcomes are generated using actual data from these trials.
In theoretical probability, probabilities are determined by mathematical reasoning.
We can calculate the probability of a tossed coin showing heads, or the probability of
rolling two dice and getting two sixes, using mathematical reasoning.
Sample space - the set(!) of all possible outcomes, S
Event - subset of S
So the probability of an event occurring is equal to:
n(E), which represents a singular(?) unique event , divided by n(S), which represents all other unique events possible.
Fair - no outcome is more likely to occur than another
P1 - huh interesting you can have an event that has a probability of 0 be apart of the sample space?
P2 - P(E’), so it seems like the ‘ symbol is used for complements and I guess sets and probability play a role together. P2 is saying that probability of one event plus the probability of every other event equals 1. Mmm. That makes sense.
P3. - the probability of two events occurring, in general, is equal to the probabilities of each individual event minus the probability of the events occurring together.
union of probabilities - when events occur in general (?)
intersection of probabilities - when events occur together(?)
Hmm:
So why are we multiplying (or I guess dividing) by 1/n(S), because originally we will have just the cardinality of various events. Specific instances. To find the probability, and get the formula shared in P3, we need to divide the specific events by the total number of possible events n(S).
Ok thats it for that section and thats it for the class today.
Huh. Something I just thought of: I think the textbook is probably a better resource for this class then the professor.
The class is done with an online textbook. It’s called Calculus and Its Applications . Honestly though, I should say the class is done entirely through the textbook. Pearson has stuff to generate homework questions, quizzes, and exams. All three that I’ve done recently come from Pearson. Pearson generates these problems based off the textbook. After looking through stuff in the textbook, if you’re goal is to pass the class I don’t think listening to the teachers lectures is valuable unless the textbook is doing a poor job of explaining something.
Luckily(?) I’m doing college for free through work, but its starting to feel like this class is just a textbook that I could’ve done myself.
You could share your work for some math problems.
Notes on 10.3 Discrete Probability Distributions:
they form a probability distribution, which
can be represented by graphing the probability of an outcome as a function of that
outcome.
turn the probability of an outcome into a function of that outcome and then graph it
Such a graph is a bar chart called a histogram.
This makes it sound like the only graph of the probability of an outcome is a bar chart/histogram. Ok.
So random variable in this context refers to a specific function. Ok. X(s) = x, where X(s) is representing some element in the sample space, s being some element in the sample space, and x being the value giving to some element s.
A random variable is a measurement used in an experiment with random outcomes
that allows us to read (or “measure”) the outcomes of the experiment. For convenience,
the notation for a random variable is often shortened to X, instead of X(s). The set of
outputs is called the range of the random variable.For example, we can define a random variable X to be the number of heads that
result after one toss of a fair coin. We have X=0 (if the coin shows a tail) or X=1 (if
the coin shows a head), and the range of X is {0, 1}. This is illustrated in the following
figure, along with examples of random variables defined for other experiments. Note
that it is possible to define more than one random variable for an experiment.
So would it go something like this X(TTT) = 0, X(TTH) = 1, X(THT) = 1, X(THH) = 2, X(HTT) = 1, X(HTH) = 2, X(HHT) = 2, X(HHH) = 3, listing the value of X: 0, 1, 1, 2, 1, 2, 2, 3. The range of X is {0,1,2,3}.
Neat.
f(x) = P(X=x) ← Probability mass function,
1.) You can’t have a negative chance. You can’t get below no chance of something happening. It either can’t happen or has some chance of happening.
2.) so f(x) outputs the probability that an event occurs
3.) ok
so the probability that an event occurs f(x) is equal to P(X=x). We will be plugging in the the range of the random variable X. So what’s P doing here. Is it representing probability? I’m a little confused.
A probability mass function is often written as a set of ordered pairs.
So X is the number is the number of heads that result. X had a range of values from {0, 1, 2, 3}. The list of values X: 0, 1, 1, 2, 1, 2, 2, 3. What do I with this.
Since the sample space deals with fair outcomes each outcome has an equal change of happening. There are 8 different outcomes.
So the input, x, was a type of outcome in this case the numbers of heads being 0. so f(0) represents that. P(X=0) represents what exactly. The probability of when the random variable X = 0? Let’s see with further problems.
f(1) = P(X=1) = 3/8, this is because out of the 8 possible outcomes three out of eight had 1 head. Ok. So it looks like P represents probability. Ok.
Looking at the final value of f. I guess this is part of the discrete nature of it? f doesn’t take in infinitely many values. In this case it just takes in 4 inputs.
Ok that’s enough for me to do the homework. I’m going to do the homework and share some problems in a separate post.
Prior to this I did two practice problems which I forgot to record to share. You do some (optional) practice problems on a section and then do a few non-practice problems to prove your “mastery” on the material. Here’s the questions, answer, and work for the two mastery questions:
I got everything more or less right for the first question, except for e it had a note to put the answer in decimal form which I didn’t read so I got that wrong.
c left blank because I saw no need to draw it. They provide the drawings every time. So I just looked for the correct one.
d left blank because it always represents the probability of something (the alternative answer choice involves saying that g(x) represents average value) and we found the value in part b.
I got everything right on the second one. No work to show for it.
One issue I ran into when I did the practice problems (the difference between practice and mastery problems is that practice problems you can get help for other than that they are the same problems) is that in question 1 it talks about the nonnegative differences between the spins. It seems like they turned any negative differences you would get into positive. I thought you would just ignore any negative differences. They seem to have taken nonnegative to mean turn all negatives into positives. So when I initially did the practice problem I got this kind of question wrong.
A different homework assignment on the same chapter called “Identify Probability Mass Functions”
I assume this uses the three rules/things that determine if a function is a probability mass function.
1.) the output of f(x) is positive
2.) the outputs of f(x) all add up to 1
3.) by definition the function deals with probability
From the practice problems:
all the outputs are positive, they all up to 1, idk how i’m supposed to know if it deals with probability or whatever but it has decimals. that seems probability-ish
ok it is a probability mass function
there is a negative out put, but the outputs do add to 1, and it does seem to deal with probabilities but since it has a negative out put its not a probability mass function
hmm. I got it wrong. I guess because the output is negative I guess that means it does not deal with probabilities because probability can’t be negative
oh yeah here’s how its having me answer:
1.) all the outputs would be positive in this equation
2.) i guess this deals with probability? its some event x divided by a total
3.) 1+5+9+13 = 28 so the probabilities add up to 1
so this is a mass function
and i got it right neat
From mastery:
1.) outputs are positive
2.) deals with probabiltiies
3.) numbers add up to 1
mass function
1.) positive
2.) deals with probabilities
3.) 3+5+7+9 = 24, the probabilities add up to 1
mass function
1.) negative outputs
2.) not dealing with probabilities
3.) does add up to 1
not a mass function since its not dealing with probabilities and has a negative output
got all three right. ok thats enough class math today.
you didn’t say what answer you gave that’s wrong so it’s kinda confusing.
