Do you play or know much about poker?
Cool. The game looks cool. I’ve downloaded steam and bought and downloaded the game.
I don’t play poker but I have played Texas Hold 'Em for fun before. I’m not unfamiliar with some of the broad ideas of poker.
Okay, I played Baba Is You for a few hours today. Steam says 3.2 hours play time but I wasn’t playing all the time the game was open. It’s pretty cool.
Feel free to share thoughts, problems or questions about Baba Is You. I could explain some concepts or give some hints.
Sure. I’m currently not having much trouble. Sometimes I get a bit stuck on a level and then go away. Then when I come back to it I usually get it in short time. It’s an interesting game. I don’t have many thoughts on it yet. I’m enjoying it.
You said in Eternity’s Thread:
Right so yes, I like it. I’m not so sure that I’m learning something yet, beyond things like how the game works and how to play it. Maybe that’s to do with my approach? Maybe it’s early in the game? It’s hard to count levels exactly but it appears I’ve done 30ish.
Next in Eternity’s Thread:
I hadn’t got the 2 inputs true one after ~19mins so have moved to trying 0, 1, 2, 3. Maybe I’ll learn something that helps with 2 inputs:
Alright, so I have solution for them all!
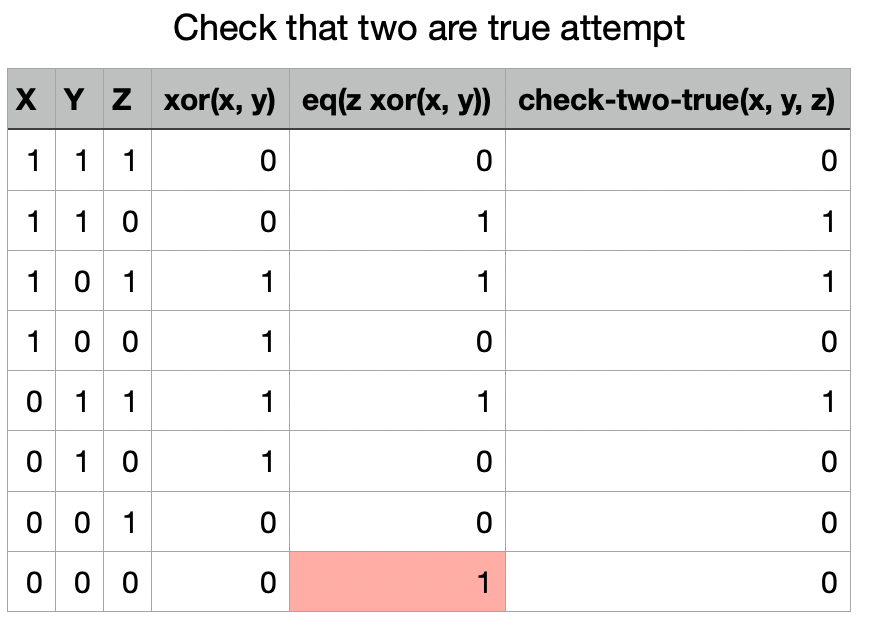
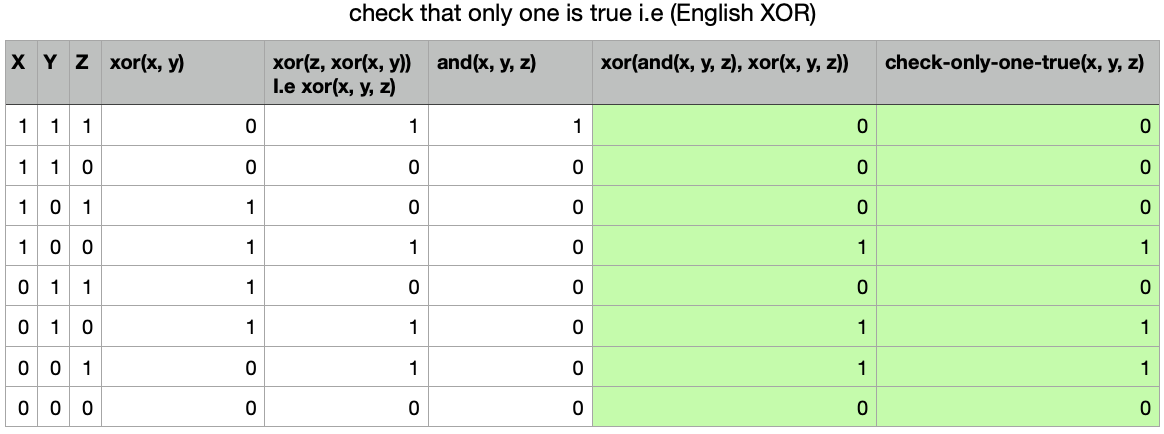
I initially tried a way to check for 2 true inputs. I was only able to get 7/8 outputs right. I then tried a way for checking for only one true input (English XOR), and I was also only able to get 7/8 outputs right(by using XOR).
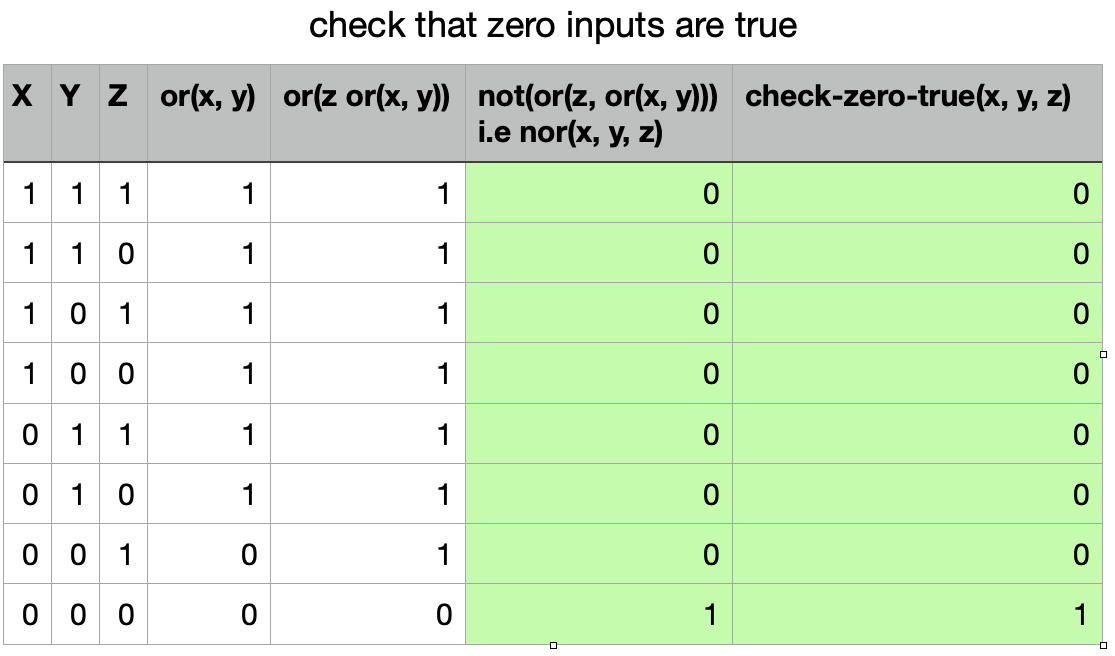
I then moved on to checking zero true inputs and got that easy: nor(x, y, z)
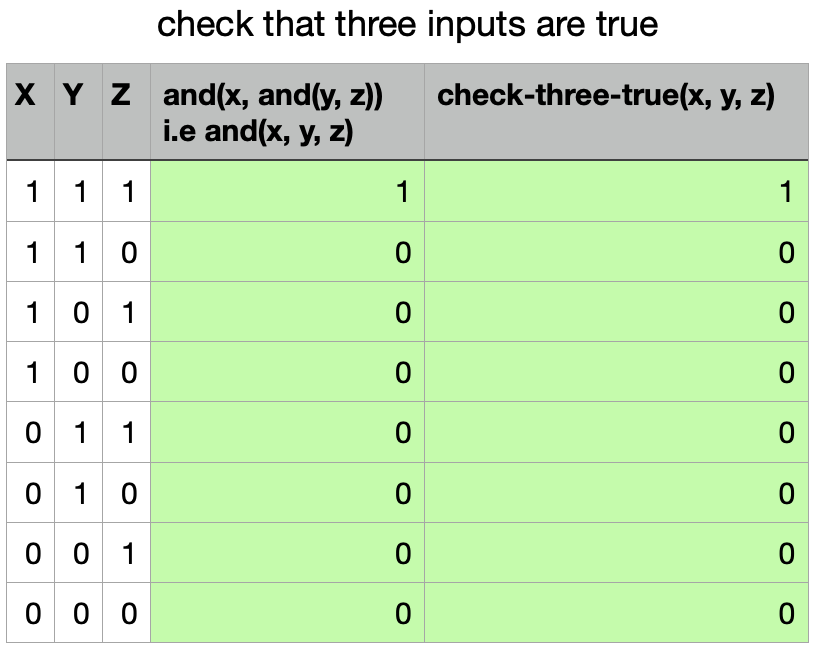
I then moved on to checking three true inputs and got that easy too: and(x, y, z)
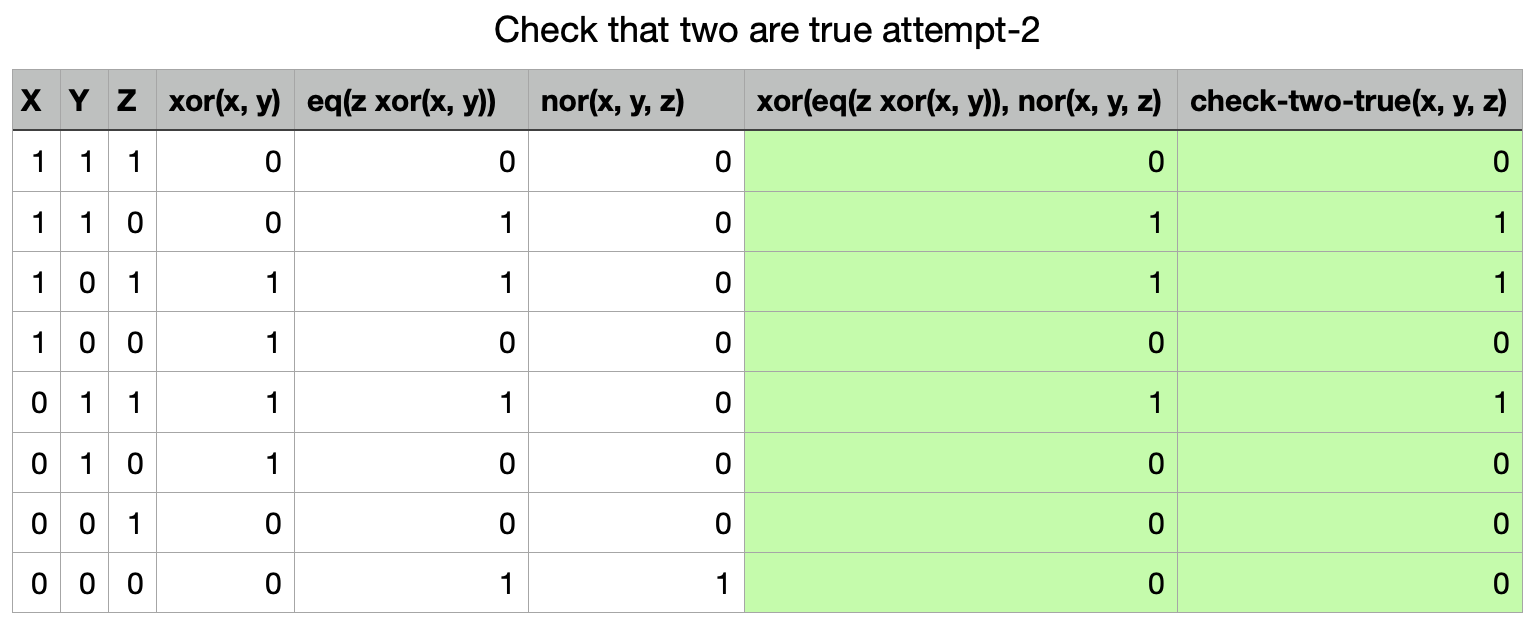
Then I realised that my results for checking 0 and 3 inputs, when xor’d with my attempts for 2 and 1 inputs respectively, allowed me to flip the remaining bit so my 2 and 1 input were correct for all input combinations!
so checking for only 2 true inputs: xor(eq(z xor(x, y)), nor(x, y, z)
and checking for only one true input (English XOR): xor(and(x, y, z), xor(x, y, z))
How did you come up with your solutions (the 7/8ths correct versions – you explained the last step)? Do they follow concepts that you can explain in English?
Why were the solutions partly wrong? Does adding on an extra step to fix them make conceptual sense or is it more like brute forcing a solution instead of using principles? Unprincipled approaches tend to stop working in harder more complex cases.
For only one input true, I knew already that xor(x, y, z) got 7/8 inputs the same as English xor.
I was searching for ways to get some combination of operators such that their truth table matched the truth table of the problem. So some guesses ended up with some expressions that got part of the way.
So I got them through primarily through manipulating truth tables and not primarily through an understanding in English of the concepts.
For two inputs true, I had the solution in the far right column and was trying to find ways to get it’s truth table using a few two input operator steps.
I think my extra step to fix them occurred to me only in the context of truth tables and finding ways to flip one bit. The extra step doesn’t necessarily make conceptual sense to me. Like, I haven’t tried example english sentences and seen how the logic works. I agree I think with problems harder than this yeah I wouldn’t succeed.
I read ahead in Eternity’s thread to see their solution. Their solution is much more elegant and intuitive I think. It made sense to me as soon as I saw it. It didn’t occur to me to approach the problem like that. We got the approx the same answers for 0 and 3. I think i’ve been relying on manipulating truth tables too much.
I think leaning too much on manipulating truth tables and not enough on understanding logic concepts in terms of english is a problem I’ve got. Do you have any assignments/suggestions/comments for working on that, or should I continue through Eternity’s thread and see how I go?
Practice putting more into English. You can do that with some recent problems or with the next ones.
From Eternity’s thread:
I already knew that xor(x xor(y z)) was another way to write xor(x, y, z), but I used the approach that Eternity used with English xor and tried:
(x^y^z)v(x^~y^~z)v(~x^y^~z)v(~x^~y^z)
In english: all of them true or x true or y true or z true. So all possible odd combinations of inputs. This makes it easy to see what inputs it will allow and still be true. I used the truth table generator to save me time making a big truth table for this when I just wanted to check if it did give the right outputs, and it does:
In the light of what I learned from Eternity’s approach, I re-approached the problem of converting OR to AND but without using truth tables except to check my answers. My previous answer, while correct, wasn’t as simple as it could be, and it was arrived at by manipulating truth tables, and not trying to understand AND and OR conceptually in terms of eachother.
I started by stating what OR is english:
OR = True if any input is true
That meant I could represent it like this:
(A^~B)v(~A^B)v(A^B)
i.e one input true, the other input true, or both true. The expression specifies all the input cases that will output true, and ORs them together. But obviously I had to use OR for that. So that wouldn’t work.
But OR also means:
OR = False if both inputs are false.
OR only outputs false in one input scenario. So if I negate that input scenario I get all the true scenarios:
~(~A^~B)
Which means in english, true if it’s not the case that both inputs are false, which is OR! So I think this is De Morgan’s first law.
Then doing the same thing for AND:
AND = true if both inputs are true and false when any inputs are false. i.e false if A is false or B is false or both
AND is only true in one input scenario, and that’s when neither A or B are false. So:
~(~Av~B)
Which means, true if it’s not the case that either A or B or both are false.
So I think this is De Morgan’s second law.
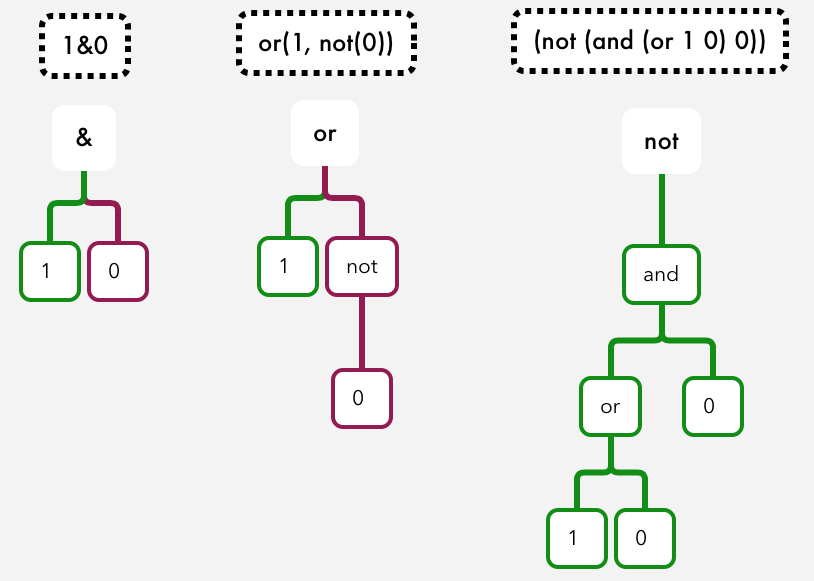
Here are the trees:
and my answers:
1&0 = 0
or(1, not(0)) = 1
(not (and (or 1 0) 0)) = 1
Evaluating using trees was fast. It was also clearer to me what each step was and it felt like I had to be less careful.
I did some practise in the same vein as above. I tried to find equivalent expressions to 2 input XOR using my understanding of the concepts in english.
xor(A, B) = ?
two input xor and xor in english means: true if and only if one input is true.
xor has two true, and two false input cases. If i specify the true input cases, the false ones will be implied:
xor(A, B) = (A^~B)v(~A^B)
That uses both true cases. It means true if just A or just B is true.
If I use both false cases:
xor(A, B) = ~((~A^~B)v(A^B))
That uses both false cases, and negates the case where either of them are true. The expression means: true if it is not the case that A and B are both true or false.
xor(A, B) = (A v B)^~(A^B)
This one shows you how ‘xor’ is like ‘or’, but with an amendment. It means: true if A or B is true but not if both are true.
Have you been writing? I don’t think you shared any for a while.
I haven’t been writing as frequently as assigned. I just tallied up my writing days since the assignment on the 01/06 and I wrote on 17 days of 41. I was writing more frequently earlier on. I have written on only two of the last 7 days.
Here is something I wrote 2 days ago:
In the TV show Alone contestants compete for a large cash prize. The USA one is often $500,000. The competition is simple. You are dropped in the wilderness alone with 10 survival items that you pick. Whoever outlasts all the other contestants wins. Contestants can voluntarily leave at any time, or they might get removed by the show’s medical team if they are deemed be at a medical risk. The contestants film themselves and only encounter the rest of the crew for routine medical checkups.
The contestants have to do whatever it takes to survive. For all the contestants, that largely involves the same things: make shelter, find water, find food. This is because keeping a human body alive is roughly the same for everyone, or at least these things are always necessary.
So the thing is the challenge is really hard. Contestants lose a lot of weight really quickly. They quickly deteriorate in most other health respects too. Some contestants bulk up before going on the show so they have a lot of fat reserves on them, because they’re expecting to partly have to out-starve other contestants. So, why is it such a hard challenge? Contestants are put in a situation that with enough time, and with no intervention, they would almost all certainly die. So how did human beings in the past ever survive in these conditions the first place? And why is modern western life not usually like that, except when we’re on a survival tv show? How is it possible that in our day-to-day western lives, we live in a world where it’s actually extremely uncommon if not difficult to die from starvation or exposure or malnutrition?
One part of the answer is that humans don’t and never have lived alone. Humans have always lived in groups, even if small groups. I’ll come back to this. But another part of the answer is cultural knowledge. These small groups were usually descendants of previous inhabitants of the area. So they passed on area-specific knowledge of things that would help them survive, like what local plants and animals are edible, or where good locations to live are, or where the good hunting and fishing spots are, how to hunt local animals, how to use local animal parts for other things. In the modern world, we don’t have a lot of that knowledge any more. Lots of that knowledge disappeared because it wasn’t needed by those groups anymore because their societies got advanced, or the small primitive groups died out because their knowledge wasn’t good enough to keep them alive under special conditions outside of their knowledge’s parochial domain.
So why does not living alone help us to survive? Well when we live in a group of people, we can cooperate. We can take advantage of the gains that we can get from a division of labour. In the modern word, we participate in a huge international division of labour. Hundreds of millions of people are involved in the modern economies of today, allowing us to benefit from the productive efforts from all of those millions of people. This social institution of the division of labour in our modern world is the explanation for why in our day to day lives the basic material conditions of our existence like food, water, shelter, are not our primary concerns. Most people don’t live in fear of starvation. The difficulty of feeding and clothing and housing oneself is trivial compared to how difficult these things are on the show Alone for this reason. Also the quality of our food, housing and clothing is far far better than you could make on Alone. On Alone, you don’t get any of the gains that you do from participating in a division of labour society (except for your initial 10 items and your exisiting survival knowledge). You must produce all that you need and only on your time. This is extraordinarily difficult and dangerous.
Two things that are really important to the functioning of the division of labour are savings and capital accumulation.
Thinking about the situation on Alone can help you understand certain things about the role these play in our modern world too. Sometimes it is said by people that capital (i.e means of production, I.e tools) only benefits its owners. In other words; that other people in a division of labour possessing capital and savings are of no benefit to you, they can only benefit their owners. This is something that Marxism claims. This is false, and we can see why when we think about a wilderness survival situation like on Alone. Say you’re alone in the wilderness and you encounter another person. Would you be in a better or worse situation if you found out that they had stockpiles of dried meats, a shelter that could fit two people, chopped firewood to last through the entire winter, and lots of hunting a fishing tools they made, or if they had nothing but a tarp and the fish they had caught that morning? Assuming they see the value in cooperation, like you do, you would both be much better off if they had lots of savings(dried meats, chopped wood) and capital (tools) accumulated. They maybe have enough food to eat such that they don’t have to go fishing this week and next. That means they can work on other things like making more fishing gear, or hunting larger animals that take more time, or building better quality houses, or thinking about how to find more people. Importantly they have strengths you don’t have, and you have strengths that they don’t have, and you can trade with them. But even if they’re way better than you at everything, you can do something that for them is a lower priority for them, so they can focus their labour on higher priority things. Your labour on something of less priority for them can free up their valuable time. In a division of labour, the savings and capital accumulation of each party serves to benefit all who engage in it. Looking at our more extensive division of labour societies with this in mind, it can help us see that this claim by Marxism is wrong here too. In a division of labour society, the savings and capital accumulated by wealthy businesses serve everybody who trades with them. You can buy their products at prices and in quantities that are only possible with their massive investments of savings and capital.
A big part of what makes Alone so hard is that you can’t cooperate with others. You can’t do division of labour with them.
I haven’t retested typing for over a month. I wasn’t improving by that much, and started avoiding practising it.
Recently I’ve been learning touch typing the numbers as an alternative to practising and testing typing speed. I’ve been doing that about 15 mins a day.
I retested just now. ~All first try without warming up.
Quotes: 66WPM 98% Acc
One Minute 63WPM 98% Acc
English 200 no punc 91WPM 100% Acc (second try)
English 200 with punc 77WPM 99% Acc
Okay so what I worked on today was continuing trying to understand operations in terms of other ones conceptually. Here are basically my notes or thoughts as I was working on it. It’s less structured but I thought I’d share anyway.
Also, I’ve found the infix notation works better for my intuitive understanding of these simpler expressions and as helped me get over some conceptual hurdles. Prefix is something I need more practise with.
how can i express implies in another way?
implies has 1 false case, and 3 true cases.
A implies B means: if A is true, then B is true, else true.
Here are the 3 true scenarios or’d together:
(A^B)v(~A^B)v(~A^~B)
This means: true if A and B are true, if A is false and B is true, or if A is false and B is false.
and the 1 false scenario:
(A^~B)
so it’s negation:
~(A^~B)
Is true. This means: true if it is not the case that A is true and B is false.
But also apparently ~A v B is equivalent. How?
Well I can convert the ‘and’ operation A^B to an equivalent ‘or’ operation by negating both A and B and the whole expression. So A^B = ~(~Av~B). This is one of De Morgans Laws.
So if we take the expression ~(A^~B), and negate (A) and (~B) and the expression we get:
~ ~(~Av~ ~B)
removing double negatives:
~A v B
Which is that answer.
Okay I can derive the expression ~A v B from ~(A^~B) using De Morgan’s Laws but can I see conceptually how they are equivalent to eachother, and equivalent to A⇒B?
Okay so what is ~A v B in words? It means: true if A is false or B is true.
A^B = ~(~Av~B)
A^B has one case in which it is true, and 3 in which it is false. The true case implies the false cases, and the false cases imply the true cases.
If it’s true that it’s raining and it’s cloudy (i.e A^B = 1), then it’s false that it’s not raining or it’s not cloudy or both (i.e ~Av~B = 0). So if someone says, it’s not raining, then thats false ( i.e ~A = 0). If they say it’s not cloudy, then thats false (i.e ~B = 0). If they say it’s neither raining nor cloudy, then thats false (i.e ~Av~B = 0). If they say it’s not the case that it’s neither raining nor cloudy nor both, that’s true (i.e ~(~A v ~B) = 1).
If it’s true that it’s cloudy or sunny or both (C v S = 1), then it’s false that it’s both not cloudy and not sunny ((~C^~S) = 0). If it’s false that it’s both not cloudy and not sunny, then it’s true that it’s not the case that it’s both not cloudy and not sunny ~(~C^~S) = 1.
Ok try to improve that and report back in around ten days